
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



gọi độ cao của vệ tinh C so với mặt đất là đoạn CH
lại có AB+BH=AH<=>AH=110+BH(4)
xét tam giác ACH vuông tại H có: \(tan83,9^o=\dfrac{CH}{AH}=>CH=AH.tan83,9^o\left(1\right)\)
xét tam giác CBH vuông tại H có: \(tan86,2^o=\dfrac{CH}{BH}=>CH=BH.tan86,2^o\left(2\right)\)
(1)(2)=>\(BH.tan86,2^o=AH.tan83,9^o\)
mà AH=110+BH(cmt)=>\(BH.tan86,2^o=\left(110+BH\right)tan83,9^o\)
\(=>BH=180,6cm\)(3)
thay (3) vào(2)=>\(CH=\)\(180,6.tan86,2^o=2719,5km\)
vậy độ cao vệ tinh C là 2719,5km

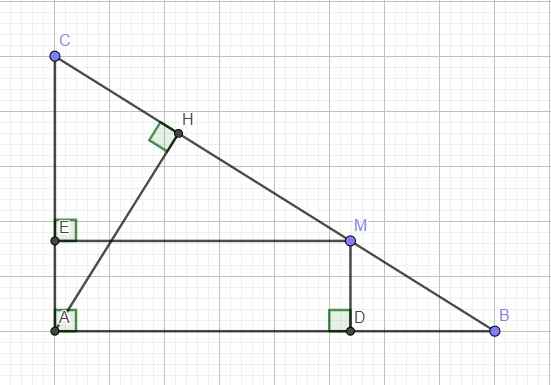
Theo giả thiết: \(ME\perp AC\Rightarrow\Delta MEA\) vuông tại E \(\Rightarrow\) E thuộc đường tròn đường kính AM (1)
Tương tự, tam giác MDA vuông tại D \(\Rightarrow\) D thuộc đường tròn đường kính AM (2)
Tam giác MHA vuông tại H \(\Rightarrow\) H thuộc đường tròn đường kính AM (3)
(1);(2);(3) \(\Rightarrow\) 5 điểm A, D, M, H, E cùng thuộc đường tròn đường kính AM (đpcm)



1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

Bài 2:
a: \(P=\sqrt{a}+2+\sqrt{a}+2=2\sqrt{a}+4\)
b: Để P=a+1 thì \(a-2\sqrt{a}-3=0\)
hay a=9
\(2,\\ a,P=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{2-\sqrt{a}}=\sqrt{a}+2+2+\sqrt{a}=2\sqrt{a}+4\\ b,P=a+1\Leftrightarrow a-2\sqrt{a}-3=0\\ \Leftrightarrow\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)=0\\ \Leftrightarrow\sqrt{a}=3\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a=9\left(tm\right)\\ 3,\\ a,ĐK:x\ge0;x\ne4\\ b,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+2}\\ c,P=2\Leftrightarrow2\sqrt{x}+4=2\sqrt{x}\\ \Leftrightarrow0\sqrt{x}=-4\Leftrightarrow x\in\varnothing\)

Câu 3:
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)




 mọi người giúp em với ạ 🥺
mọi người giúp em với ạ 🥺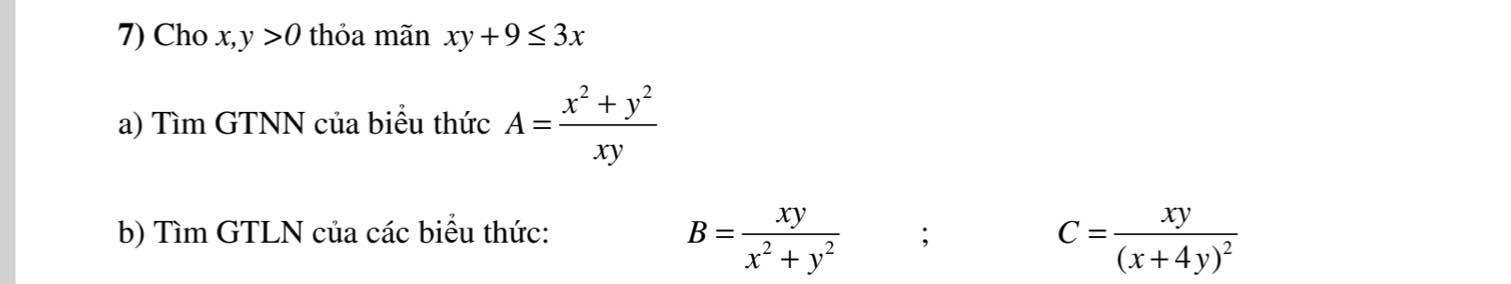 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺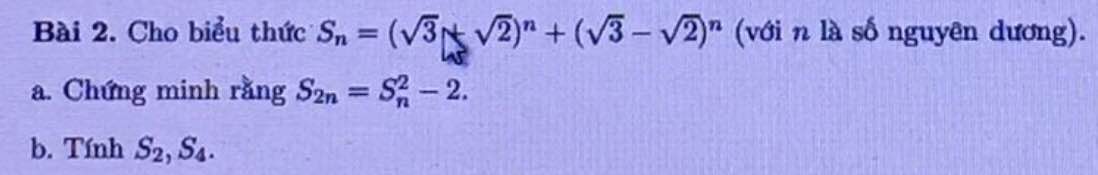 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺


