
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f'\left(x\right)=-sinx\Rightarrow f'\left(\dfrac{\pi}{4}\right)=-sin\left(\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
\(g'\left(x\right)=-\dfrac{1}{cos^2x}\Rightarrow g'\left(\dfrac{\pi}{4}\right)=-\dfrac{1}{cos^2\left(\dfrac{\pi}{4}\right)}=-2\)
\(\Rightarrow\dfrac{f'\left(\dfrac{\pi}{4}\right)}{g'\left(\dfrac{\pi}{4}\right)}=\dfrac{\sqrt{2}}{4}\)

2.
\(\Leftrightarrow cos2x-cos8x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow2sin5x.sin3x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin3x\left(2sin5x-1\right)-cos5x\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos5x\right)\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=sin3x=cos\left(\dfrac{\pi}{2}-3x\right)\\sin5x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=3x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{\pi}{6}+k2\pi\\5x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
3.
\(\Leftrightarrow1+sinx=cosx-cos3x+2sinx.cosx+1-2sin^2x\)
\(\Leftrightarrow sinx=2sin2x.sinx+2sinx.cosx-2sin^2x\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\1=2sin2x+2cosx-2sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4sinx.cosx+2cosx-2sinx-1=0\)
\(\Leftrightarrow2cosx\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2cosx+1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

3:
a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SBC) vuông góc (SAB)

ĐK: `x \ne kπ`
`cot(x-π/4)+cot(π/2-x)=0`
`<=>cot(x-π/4)=-cot(π/2-x)`
`<=>cot(x-π/4)=cot(x-π/2)`
`<=> x-π/4=x-π/2+kπ`
`<=>0x=-π/4+kπ` (VN)
Vậy PTVN.

4.
b, \(2sin^2\dfrac{x}{2}-5sin\dfrac{x}{2}+3=0\)
\(\Leftrightarrow\left(sin\dfrac{x}{2}-1\right)\left(2sin\dfrac{x}{2}-3\right)=0\)
\(\Leftrightarrow sin\dfrac{x}{2}=1\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\pi+k2\pi\)
3.
a, \(3cos^2\dfrac{x}{2}-4cos\dfrac{x}{2}+1=0\)
\(\Leftrightarrow\left(cos\dfrac{x}{2}-1\right)\left(3cos\dfrac{x}{2}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\dfrac{x}{2}=1\\cos\dfrac{x}{2}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\pm2arccos\dfrac{1}{3}+k2\pi\end{matrix}\right.\)






 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(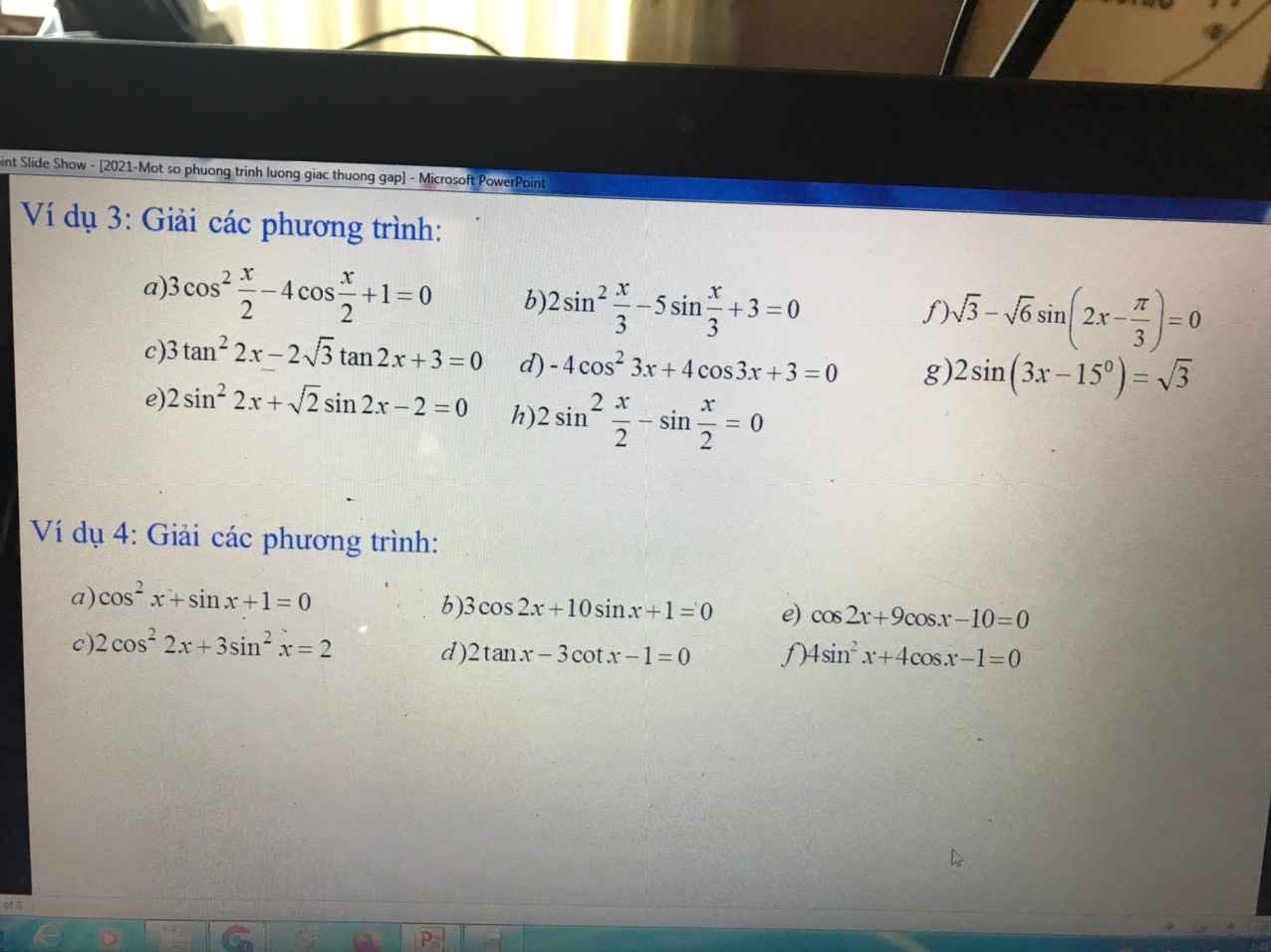
Bạn cần giúp câu nào nhỉ?
Nếu cần hết thì nên chia nhỏ từng câu ra, nhiều quá người khác nhìn sẽ bị ngộp, không ai muốn làm đâu
câu 1 A,B ạ