Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2021a}{2021b}=\dfrac{2021a-c}{2021b-d}\)
c, Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2\)
Áp dụng t/c dtsbn:
\(\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)



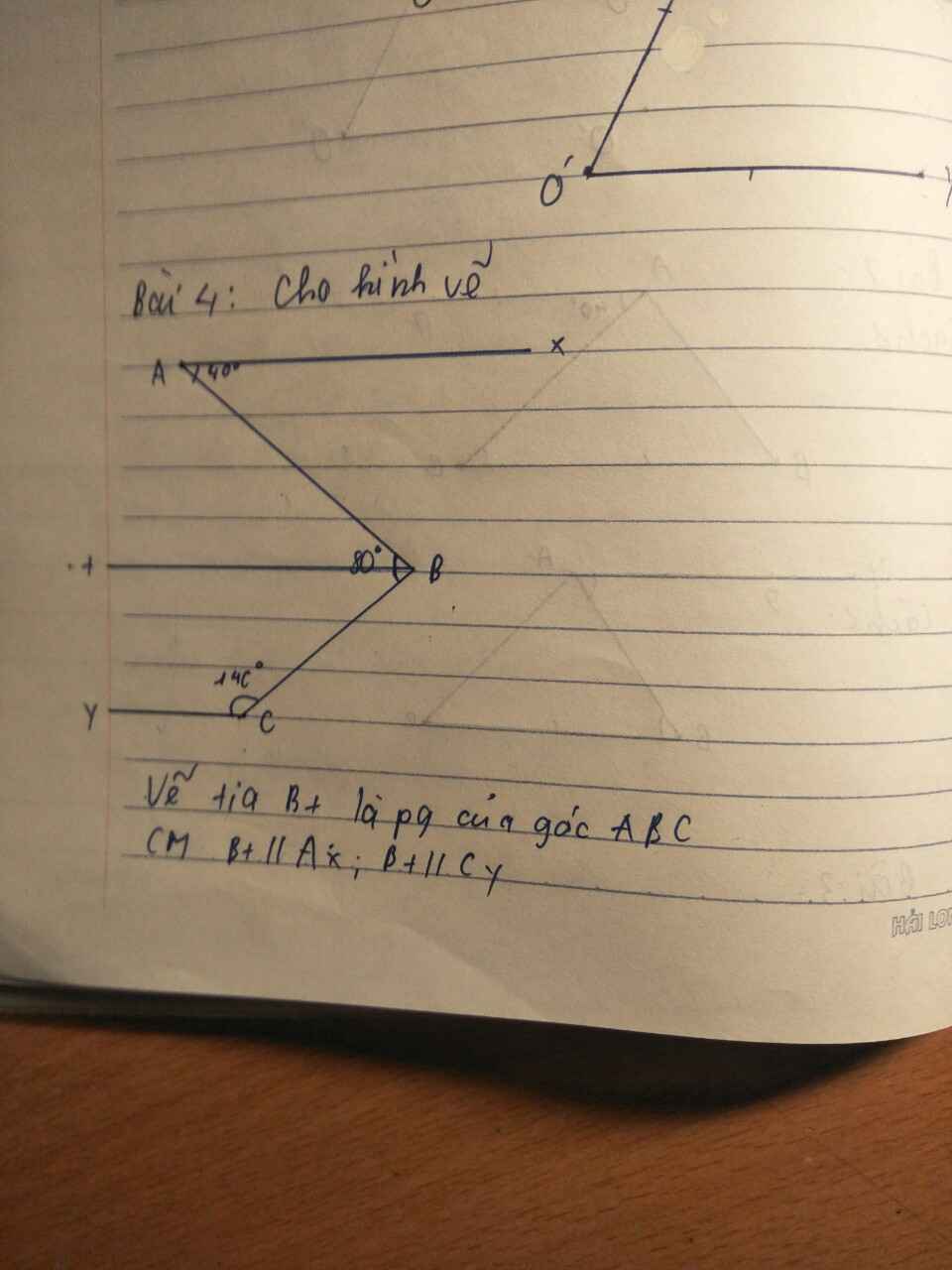
Ta có: Bt là tia p/g của \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABt}=\widehat{CBt}=\dfrac{\widehat{ABC}}{2}=80^0:2=40^0\)
Ta lại có: \(\widehat{BAx}=\widehat{ABt}=40^0\) (so le trong)
⇒Bt//Ax
Kẻ Ca là tia đối của Cy
Lại có: \(\widehat{BCa}\) kề bù với \(\widehat{BCy}\)
\(\Rightarrow\widehat{BCa}+\widehat{BCy}=180^0\)
\(\Rightarrow\widehat{BCa}+40^0=180^0\)
\(\Rightarrow\widehat{BCa}=140^0\)
Mà \(\widehat{CBt}=\widehat{BCa}=40^0\) và 2 góc này so le trong
Ca//Bt hay Cy//Bt
ôi cảm ơn bạn nhoa !!!
chúc bạn một buổi tối tốt lành :>>>


Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow1+\dfrac{b}{a}=1+\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\\\dfrac{a}{c}=\dfrac{b}{d}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{a}{c}\right)^2=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\\\left(\dfrac{a}{c}\right)^2=\dfrac{ab}{cd}\end{matrix}\right.\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)




bn làm r mà.
m, cf m fcmk