Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM
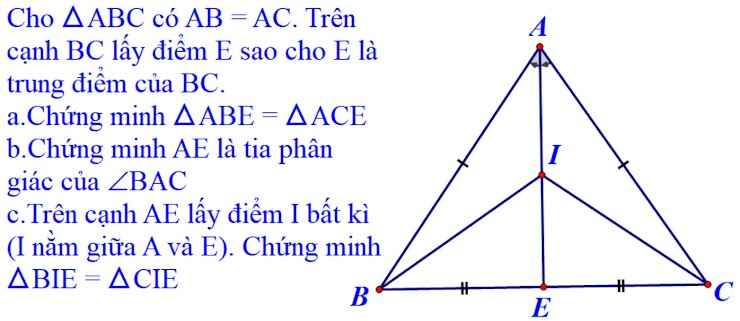
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).
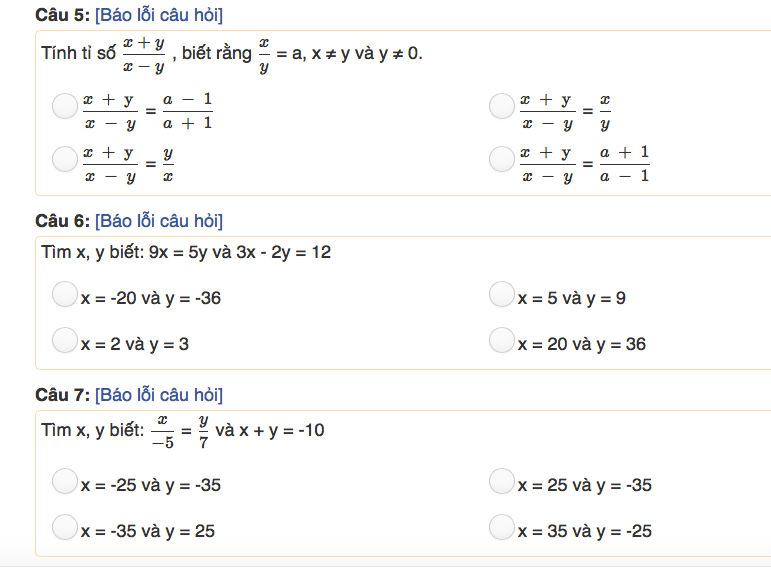
Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB
Bài 3:
d: Ta có: \(5^{\left(x-2\right)\left(x+3\right)}=1\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
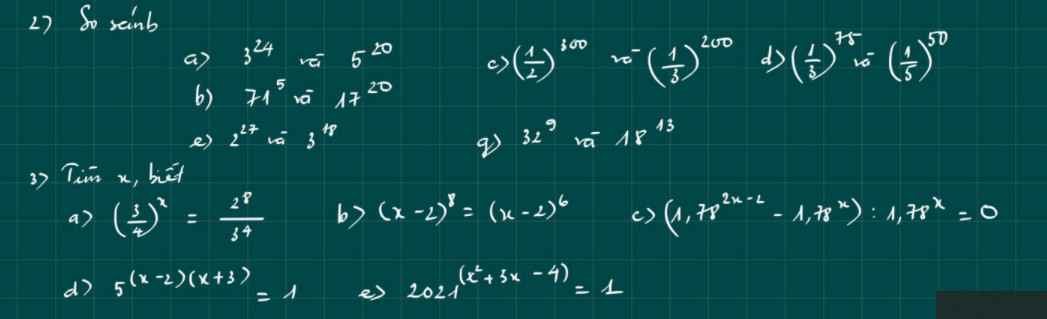
Tỉ lệ \(x=\dfrac{y}{-5}\)
x -4 -1 2 3
y 20 5 -10 -15