Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng quy tắc hợp lực song song cùng chiều.
Ta có: P= PA + PB = 1000N (1)
Mặt khác: PA. OA = PB. OB
=> =
=
=
(2)
(1) & (2) => PA = 600N và PB= 400N

Áp dung quy tắc hợp lực song song: \(\frac{F_1}{F_2}=\frac{d_2}{d_1}=\frac{40}{60}=\frac{2}{3}\)(1)
Mà \(F_1+F_2=P=1000N\) (2)
Từ (1) và (2) suy ra \(\begin{cases}F_1=400N\\F_2=600N\end{cases}\)

Chọn B.
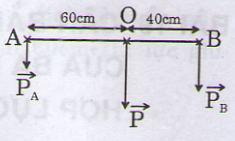
Gọi F1, F2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d1 = 60 cm, d2 = 40 cm.
Ta có: F1 + F2 = mg = 1000 (1)
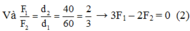
Từ (1) và (2) → F1 = 400 N, F2 = 600 N.

Chọn B.
Gọi F 1 , F 2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d 1 = 60 cm, d 2 = 40 cm.
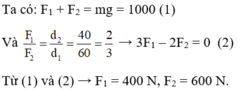

Gọi P1 là lực tác dụng lên vai người đi trước, P2 là lực tác dụng lên vai người đi sau, ta đã có: d1 = OO1 = 60 cm; d2 = OO2 = 40 cm.
Áp dụng quy tắc hợp lực hai lực song song cùng chiều ta được:
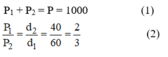
Giải hệ (1) và (2) ta được: P1 = 400 N, P2 = 600 N
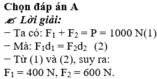


Gọi \(F_1;F_2\) lần lượt là các lực mà vai của người thứ nhất và hai chịu.
Theo quy tắc Momen lực ta có:
\(d_1\cdot F_1=d_2\cdot F_2\)
\(\Rightarrow60\cdot F_1=40\cdot F_2\left(1\right)\)
Mà \(F_1+F_2=1000\left(2\right)\)
Từ (1|) và (2) \(\Rightarrow\left\{{}\begin{matrix}F_1=400N\\F_2=600N\end{matrix}\right.\)