
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI


a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
b,c: góc FAE+góc FHE=180 độ
=>FAEH nội tiếp
=>góc HFE=góc HAE=góc C
Xét ΔHFE vuông tại H và ΔHCA vuông tại H có
góc HFE=góc HCA
=>ΔHFE đồng dạng với ΔHCA
=>HF/HC=HE/HA
=>HF*HA=HC*HE

a: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{DAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔADM=ΔCBN
Suy ra: DM=BN

\(\left(a+b+c\right)^2\)
\(\Rightarrow\left[\left(a+b\right)+c\right]^2\)
\(\Rightarrow\left(a+b\right)^2+2c\left(a+b\right)+c^2\)
\(\Rightarrow a^2+2ab+b^2+2ca+2bc+c^2\)
\(\Rightarrow a^2+b^2+c^2+2ab+2bc+2ca\)
\(\left(a-b-c\right)^2\)
\(\Rightarrow\left[\left(a-b\right)-c\right]^2\)
\(\Rightarrow\left(a-b\right)^2-2c\left(a-b\right)+c^2\)
\(\Rightarrow a^2-2ab+b^2-2ca+2bc+c^2\)
\(\Rightarrow a^2+b^2+c^2-2ab+2bc-2ca\)
ta có (a+b+c)^2 = (a+b+c).(a+b+c) =a^2+ab+ac+ab+b^2+bc+ac+bc+c^2 = a^2+b^2+c^2+2ab+2ac+2bc
và (a-b-c)^2 = (a-b-c)(a-b-c) = a^2-ab-ac-(ab-b^2-bc)-(ac-cb-c^2) =a^2-ab-ac-ab+b^2+bc-ac+cb+c^2=a^2 -2ab-2ac+bc+b^2+c^2

Em cần giúp câu nào hả em? Em nên chụp 1-2 ý cho 1 lần hỏi nhá, như thế mọi người sẽ dễ dàng giúp em hơn
13
a, \(3x-4=-x+8\)
\(< =>3x+x=8+4\)
\(< =>4x=12\)
\(< =>x=\frac{12}{4}=3\)
b, \(\frac{2x+1}{6}+\frac{x-7}{12}=10\)
\(< =>\frac{2\left(2x+1\right)}{12}+\frac{x-7}{12}=\frac{120}{12}\)
\(< =>4x+2+x-7=120\)
\(< =>5x=120+5=125\)
\(< =>x=\frac{125}{5}=\frac{5^3}{5}=5^2=25\)


 Giúp mk với mọi người ơi mk đang cần gấp cảm ơn mọi người nhé
Giúp mk với mọi người ơi mk đang cần gấp cảm ơn mọi người nhé






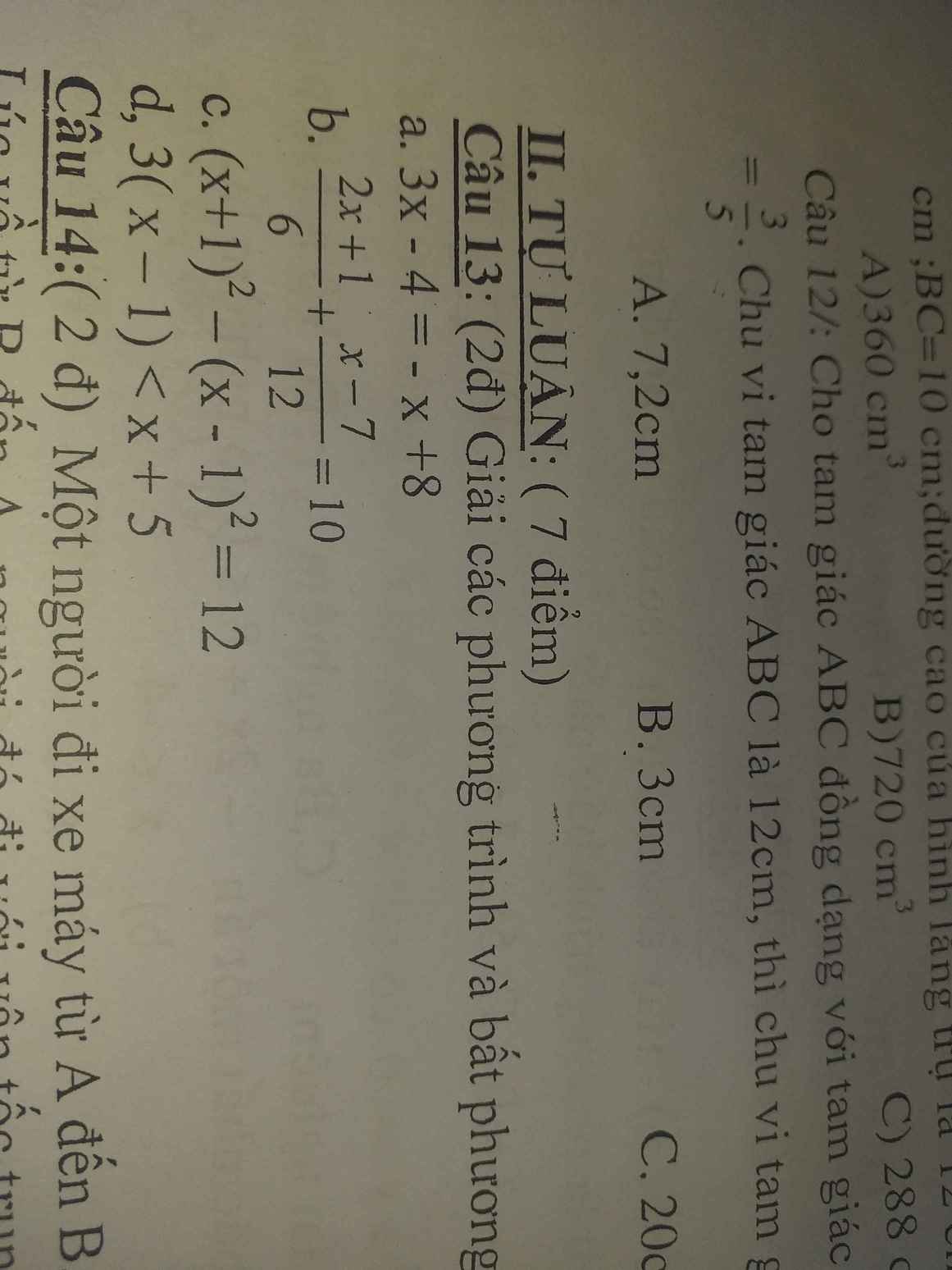

a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI