Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ M=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)
anh có thể ghi thêm các bước trước khi ra đc mấy cái này ko ạ tại rút gọn quá e ch hỉu ạ e c.ơn


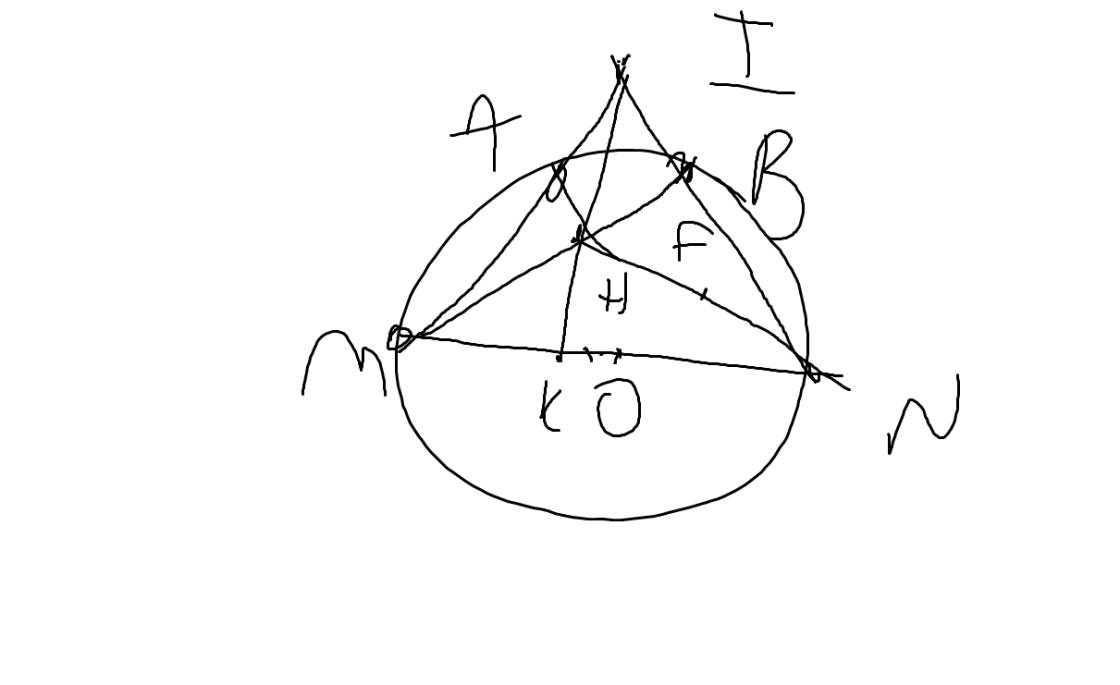
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN

\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)

Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

a: Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)
b:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=6^2-3^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{6}\)
=>\(\dfrac{AD}{1}=\dfrac{CD}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{1}=\dfrac{CD}{2}=\dfrac{AD+CD}{1+2}=\dfrac{3\sqrt{3}}{3}=\sqrt{3}\)
=>\(\left\{{}\begin{matrix}AD=\sqrt{3}\simeq1,7\left(cm\right)\\CD=2\sqrt{3}\simeq3,5\left(cm\right)\end{matrix}\right.\)
c: ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot6=3\cdot3\sqrt{3}=9\sqrt{3}\)
=>\(AH=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
d: ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\left(1\right)\)
ΔADB vuông tại A có AE là đường cao
nên \(BE\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BE\cdot BD\)
=>\(\dfrac{BH}{BD}=\dfrac{BE}{BC}\)
Xét ΔBHE và ΔBDC có
BH/BD=BE/BC
\(\widehat{HBE}\) chung
Do đó: ΔBHE đồng dạng với ΔBDC


1)
\(=\left(6\sqrt{2}-5\sqrt{2}+3\sqrt{2}\right):\sqrt{2}=4\sqrt{2}:\sqrt{2}=4\)
2)
\(=16a-2a+5a=19a\)
3)
\(=\dfrac{2\left(2-\sqrt{3}\right)}{\left(2
+\sqrt{3}\right)\left(2-\sqrt{3}\right)}-\dfrac{3\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(\sqrt{3}+2\right)}\)
\(=4-2\sqrt{3}-6-3\sqrt{3}=-2-5\sqrt{3}\)
\(1,=\left(6\sqrt{2}-5\sqrt{2}+3\sqrt{2}\right):\sqrt{2}=4\sqrt{2}:\sqrt{2}=4\\ 2,=\left|4a\right|-2\left|a\right|+5a=4a-2a+5a=7a\left(a\ge0\right)\\ 3,=\dfrac{4-2\sqrt{3}-6-3\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=\dfrac{-5\sqrt{3}-2}{4-3}=-5\sqrt{3}-2\\ 4,=\sqrt{\left(3-\sqrt{5}\right)^2\left(3+\sqrt{5}\right)}+\sqrt{\left(3+\sqrt{5}\right)^2\left(3-\sqrt{5}\right)}\\ =\sqrt{4\left(3-\sqrt{5}\right)}+\sqrt{4\left(3+\sqrt{5}\right)}\\ =2\sqrt{3-\sqrt{5}}+2\sqrt{3+\sqrt{5}}=2\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)\\ =2\left(\sqrt{\dfrac{6-2\sqrt{5}}{2}}+\sqrt{\dfrac{6+2\sqrt{5}}{2}}\right)\\ =2\left(\dfrac{\sqrt{5}-1}{\sqrt{2}}+\dfrac{\sqrt{5}+1}{\sqrt{2}}\right)\\ =2\cdot\dfrac{2\sqrt{5}}{\sqrt{2}}=2\sqrt{10}\)

36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C


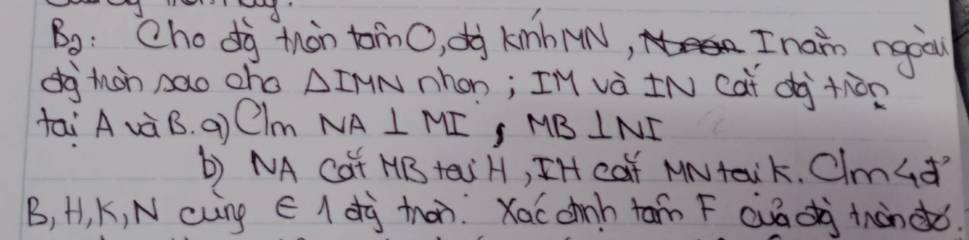

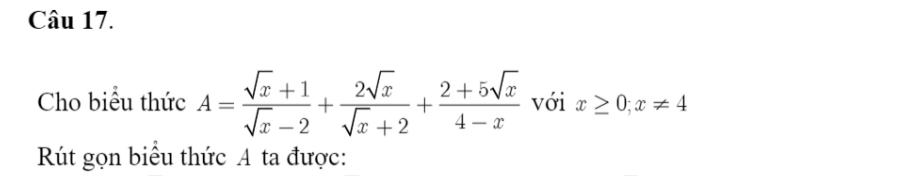

 giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.