
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm

Ta có \(x.\left(x^2+x+1\right)-x^2.\left(1+x\right)-x-7\)
\(=x^3+x^2+x-x^2-x^3-x-7\)
\(=\left(x^3-x^3\right)-\left(x^2-x^2\right)-\left(x-x\right)-7\)
\(=-7\)
Do đó giá trị của biểu thức không phụ thuộc vào biến
Vậy...

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=BC/BC=AC/HA
=>AB*AH=AC*HB
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>IH/HB=IA/AB
=>IH/3=IA/5=(IH+IA)/(3+5)=4/8=1/2
=>IH=1,5cm; IA=2,5cm

a: \(P=\left(\dfrac{-\left(x+3\right)}{x-3}+\dfrac{x-3}{x+3}+\dfrac{4x^2}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+1-x-3}{x+3}\)
\(=\dfrac{-x^2-6x-9+x^2-6x+9+4x^2}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x-2}\)
\(=\dfrac{4x^2-12x}{\left(x-3\right)}\cdot\dfrac{1}{x-2}=\dfrac{4x}{x-2}\)
b: 2x^2-5x+2=0
=>2x^2-4x-x+2=0
=>(x-2)(2x-1)=0
=>x=1/2(nhận) hoặc x=2(loại)
Khi x=1/2 thì \(P=\dfrac{4\cdot\dfrac{1}{2}}{\dfrac{1}{2}-2}=2:\dfrac{-3}{2}=-\dfrac{4}{3}\)
c: ĐểP nguyên thì 4x-8+8 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
=>\(x\in\left\{1;4;0;6;-2;10;-6\right\}\)

\(P=\left(\dfrac{x^2+1}{x^2-9}-\dfrac{x}{x+3}+\dfrac{5}{3-x}\right):\left(\dfrac{2x+10}{x+3}-1\right)\)
\(=\left(\dfrac{x^2+1}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{5\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10}{x+3}-\dfrac{x+3}{x+3}\right)\)
\(=\left(\dfrac{x^2+1-x^2+3x-5x-15}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\left(\dfrac{-2x-14}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{x+7}{x+3}\right)\)
\(=\dfrac{-2\left(x+7\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{x+7}\)
\(=\dfrac{-2}{x-3}\)
đk : x khác -3 ; 3 ; -7
\(P=\left(\dfrac{x^2+1+x\left(x-3\right)+5x+15}{x^2-9}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\dfrac{2x^2+1+2x+15}{x^2-9}:\dfrac{x+7}{x+3}=\dfrac{2x^2+2x+16}{\left(x-3\right)\left(x+7\right)}\)


PT: \(CaCO_3\underrightarrow{t^o}CaO+CO_2\) (Chất rắn sau pư là CaO)
Khối lượng CaCO3 tham gia pư là: \(m_{CaCO_3}=100.50\%=50\left(g\right)\)
=> Khối lượng tạp chất là: 100 - 50 = 50 (g)
=> Số mol CaCO3 tham gia pư là\(n_{CaCO_3}=\frac{50}{100}=0,5\left(mol\right)\)
Theo pt: \(n_{CaO}=n_{CaCO_3}=0,5\left(mol\right)\)
=> Khối lượng CaO tạo thành là: \(m_{CaO}=0,5.56=28\left(g\right)\)
Vậy: Khối lượng chất rắn sau pư kể cả tạp chất là: 28+50= 78(g)
=.= hk tốt!!
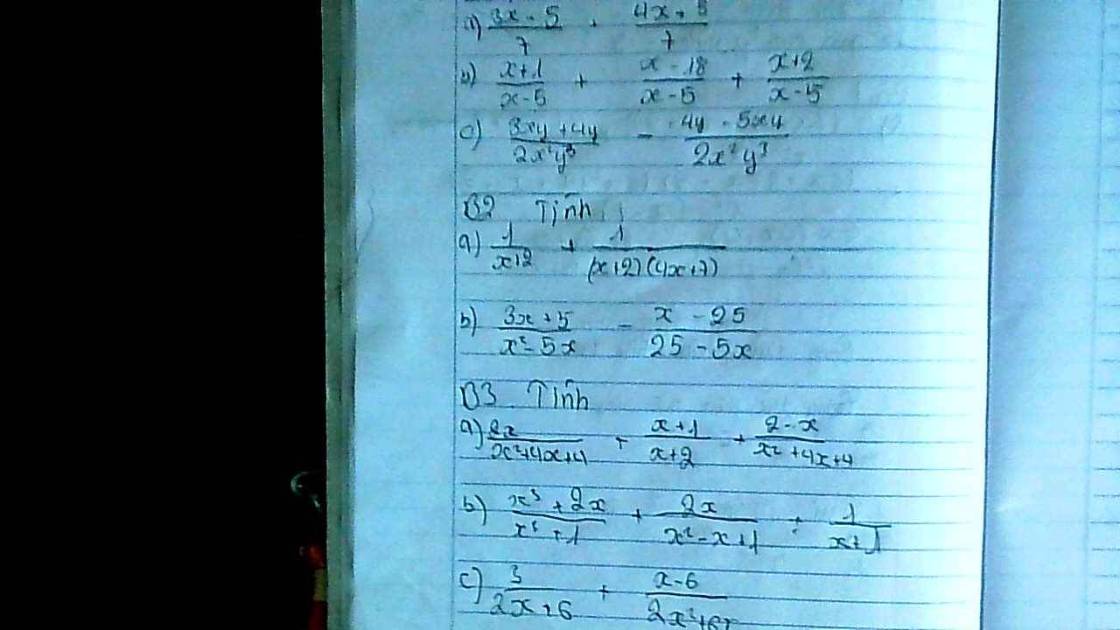
 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
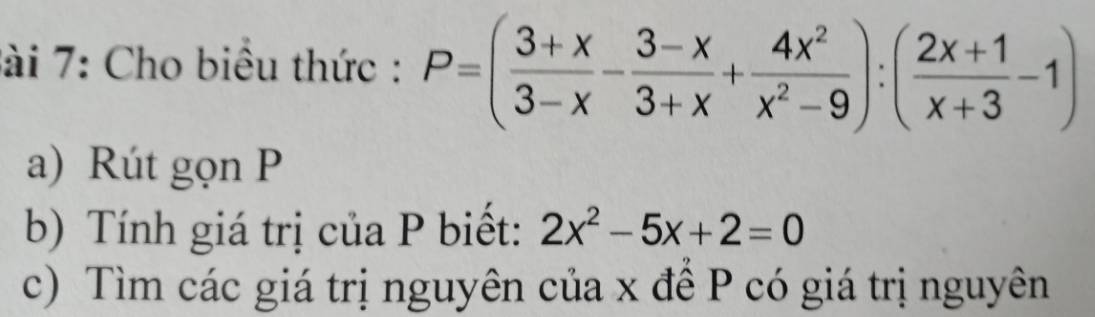
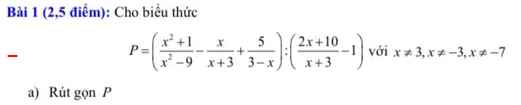

B2:
a) \(\dfrac{1}{x+2}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\left(ĐK:x\ne-2;x\ne-\dfrac{7}{4}\right)\)
\(=\dfrac{4x+7}{\left(x+2\right)\left(4x+7\right)}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+8}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4\left(x+2\right)}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4}{4x+7}\)
b) \(\dfrac{3x+5}{x^2-5x}-\dfrac{x-25}{25-5x}\left(ĐK:x\ne0;x\ne5\right)\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5x-25}\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{5\left(3x+5\right)}{5x\left(x-5\right)}+\dfrac{x\left(x-25\right)}{5x\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-10x+25}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-2\cdot x\cdot5+5^2}{5x\left(x-5\right)}\)
\(=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}\)
\(=\dfrac{x-5}{5x}\)