Công suất định mức của bóng đèn:  P = U I = U 2 R = 24 2 9 = 64 W

Đáp án: D

Tóm tắt:

\(I=0,2A\)

\(U=3,6V\)

______

\(R=?\Omega\)

Điện trở của bóng đèn sáng bình thường:

\(R=\dfrac{U}{I}=\dfrac{3,6}{0,2}=18\Omega\)

⇒ Chọn B

R=U/I=3,6/0,2=18 (Ω)

Chọn B

Điện trở của đèn là:

 \(R=\dfrac{U}{I}=\dfrac{24}{0,75}=32\left(\Omega\right)\)

Công suất điện của bóng đèn khi đó: 

\(P=U.I=24.0,75=18\left(W\right)\)

Đèn được mắc song song với phần R 1 của biến trở và đoạn mạch song song này được mắc nối tiếp với phần còn lại  R 2  ( R 2  = 16 –  R 1 ) của biến trở.

Để đèn sáng bình thường thì hiệu điện thế ở hai đầu đoạn mạch song song là U Đ = 6V và do đó hiệu điện thế ở hai đầu phần còn lại của biến Hình 11.3 trở là:

U 2  = U –  U Đ  = 12 – 6 = 6V.

Điện trở của đèn là: R Đ  =  U Đ  / I Đ  = 6/0,75 = 8Ω

Vì cụm đoạn mạch (đèn // R 1 ) nối tiếp với R 2  nên ta có hệ thức: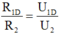

(R1D là điện trở tương đương của đoạn mạch đèn //  R 1  và U 1 D  = U 1  = U Đ  = 6V)

Mắc bóng đèn nối tiếp với biến trở, đèn sáng bình thường khi:

I b = I Đ  = I = 0,75A

U b + U Đ  = U và U Đ  = 6V → U b  = U –  U Đ  = 12 – 6 = 6V

Điện trở của biến trở là: R b  =  U b  / I b  = 6/0,75 = 8Ω

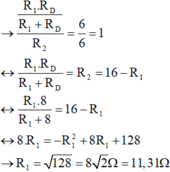
Mắc bóng đèn nối tiếp với biến trở, đèn sáng bình thường khi:

I b = I Đ  = I = 0,75A

U b + U Đ  = U và U Đ  = 6V → U b  = U –  U Đ  = 12 – 6 = 6V

Điện trở của biến trở là: R b  =  U b  / I b  = 6/0,75 = 8Ω

Sơ đồ bạn đã cho có thể hiểu như trên ( phần còn lại của biến trở là R2).
Đèn sáng bình thường khi U_đ = 6V; I_đ = 0,75A
Theo sơ đồ, ta thấy [đèn // R1] cùng nối tiếp R2 nên ta có:
I_1đ = I_2 <=> I_1 + I_đ = I_2
<=> U1:R1 + 0,75 = U2:R2
mà U1=U_đ=6V;
U2=U - U1=12-6=6V ; 
R2=16 - R1
nên 6:R1 + 0,75 = 6 : (16 - R1)
Rút gọn được : 96 - 0,75.R1^2 = 0 
Đến đây bạn giải phương trình ra , sẽ được kết quả là R1 xấp xĩ 11,3 ôm

Tóm tắt :\(R=16\left(\Omega\right);I_{Đm}=0,75\left(A\right);U=9\left(V\right)\)

Những điều cần tính:\(a,U_{Đm}=?\left(V\right);b,I=?\left(A\right);\)Độ sáng của bóng đèn so với bình thường?

a,Hiệu điện thế đặt vào 2 đầu bóng đèn lúc nó sáng bth

\(U_{Đm}=I_{Đm}\cdot R=0,75\cdot16=12\left(V\right)\)

b, Vì \(U< U_{Đm}\left(9< 12\right)\)

Nên đèn sáng yếu hơn so với bình thường

Cường độ dòng điện qua đèn khi đó:

\(I=\dfrac{U}{R}=\dfrac{9}{16}=0,5625\left(\Omega\right)\)

a) Hiệu điện thế đặt vào 2 đầu bóng đèn : 

U = I . R = 0,8 .12 = 9,6V

b) Cường độ dòng điện 9V khi đó là 

I = U/R = 9/12 = 0,75A

R1 nt Rb

a, de den sang bth\(\Rightarrow I=I1=Ib=1A\Leftrightarrow Rtd=R1+Rb=\dfrac{U}{I}=12\Rightarrow Rb=12-R1=12-6=6\Omega\)

b,\(\Rightarrow R=\dfrac{pl}{S}\Rightarrow S=\dfrac{pl}{R}=\dfrac{100.0,4.10^{-6}}{25}=1,6mm^2\)

cảm ơn bạn