a)

Ta ký hiệu canô là (1), nước là (2), bờ sông là (3)

Áp dụng công thức cộng vận tốc: 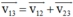 (0,25 đ)

Khi canô xuôi dòng: 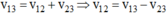 (0,50 đ)

Mà 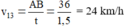 (0,25đ)

Vậy vận tốc của canô đối với nước: v 12  = 24 – 6 = 18 km/h (0,25đ)

b) Khi ca nô đi ngược dòng:

v 13  = v 12  - v 23  (0,25đ)

= 18 - 6 = 12 km/h (0,25đ)

Vậy thời gian ngược dòng của canô: 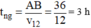 (0,25đ)

a) Gọi: (0,25 điểm)

(1): canô (2): nước (3): bờ sông

Áp dụng công thức cộng vận tốc: 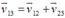 (0,25 điểm)

Khi canô xuôi dòng:

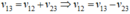 (0,25 điểm)

Mà 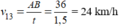 (0,25 điểm)

Vậy vận tốc của canô đối với nước: v 12  = 24 – 6 = 18 km/h (0,25 điểm)

b) khi ca nô đi ngược dòng: v 13 = v 12  - v 23  (0,25 điểm)

= 18 - 6 = 12 km/h (0,25 điểm)

Vậy thời gian ngược dòng của canô: 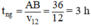 (0,25 điểm)

Chọn B.

Gọi t và t’ lần lượt là thời gian đi xuôi dòng và thời gian đi ngược dòng.

Độ lớn vận tốc của canô đối với bờ khi đi xuôi dòng và khi đi ngược dòng lần lượt là:

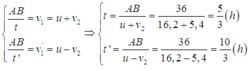
=> t + t’ = 5 (h).

Chọn C.

Độ lớn vận tốc của canô đối với bờ khi đi xuôi dòng:

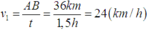
Độ lớn vận tốc của canô đối với nước:

Độ lớn vận tốc của canô đối với bờ khi đi ngược dòng và thời gian đi từ B đến A lần lượt là:

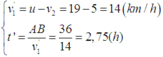
Gọi \(\left(1\right)\) : canô

       \(\left(2\right)\) : nước

       \(\left(3\right)\) : bờ

Vận tốc khi xuôi dòng là : \(40:1=40\left(km/h\right)\)

Vận tốc khi ngược dòng là : \(40:1,25=32\left(km/h\right)\)

Ta có : \(\overrightarrow{V_{13}}=\overrightarrow{V_{12}}+\overrightarrow{V_{23}}\)

\(TH_1:\) \(\overrightarrow{V_{12}}\uparrow\uparrow\overrightarrow{V_{23}}\) \(\Rightarrow V_{13}=V_{12}+V_{23}=40\)

\(TH_2:\overrightarrow{V_{12}}\uparrow\downarrow\overrightarrow{V_{23}}\Rightarrow V_{13}=V_{12}+V_{23}=32\)

Từ 2TH, ta suy ra : \(\left\{{}\begin{matrix}V_{12}=36\left(km/h\right)\\V_{23}=4\left(km/h\right)\end{matrix}\right.\)

Vậy ...

Gọi vận tốc cano cần tìm là x(km/h)

Vận tốc cano xd là x + y(km/h)

Khi nd là x-y(km/h)

Cả quãng đường xuôi lẫn ngực dòng là 40 nên ta có

\(v_{xd}.t_1=s \Leftrightarrow\left(x+y\right).1=40\Leftrightarrow x+y=40\\ v_{nd}t_2=s\Leftrightarrow\left(x-y\right).\dfrac{5}{4}=40\Leftrightarrow x-y=32\) 

\(\Leftrightarrow\left\{{}\begin{matrix}x=36\\y=4\end{matrix}\right.\)

- Khi xuôi dòng: \(v_{xd}=v_c+v_n=10+5=15\left(\dfrac{km}{h}\right)\)

Thời gian đi xuôi dòng: \(t_{xd}=\dfrac{AB}{v_{xd}}=\dfrac{18}{15}=1,2\left(h\right)\)

- Khi ngược dòng: \(v_{nd}=v_c-v_n=10-5=5\left(\dfrac{km}{h}\right)\)

Thời gian đi ngược dòng: \(t_{nd}=\dfrac{AB}{v_{nd}}=\dfrac{18}{5}=3,6\left(h\right)\)

Vậy tổng thơi gian đi là: \(t=t_{xd}+t_{nd}=1,2+3,6=4,8\left(h\right)\)

Giải: Gọi v 13  là vận tốc của ca nô với bờ; v 23   là vận tốc của nước với bờ bằng 6 km/h; v 12   là vận tốc của ca nô so với dòng nước

a. Theo bài ra ta có  v 13 = S t = 54 3 = 18 k m / h

Khi xuôi dòng: v 13   =   v 12 ­   +   v 23   ⇒ 18 = v 12 + 6 ⇒ v 12 = 12 k m / h

b. Khi ngược dòng: v ’ 13   =   v 12 ­   -   v 23 =   12   -   6 =   6 k m / h   t ' = S v 13 ' = 54 6 = 9 h