Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Khi \(W_đ=3W_t\Rightarrow W=4W_t\Rightarrow x=\pm\frac{A}{2}\)
+ Khi \(W_đ=\frac{1}{3}W_t\Rightarrow W=\frac{4}{3}W_t\Rightarrow x=\pm\frac{\sqrt{3}}{2}A\)
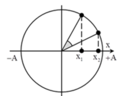
Ta có véc tơ quay như sau:
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(t=\frac{30}{360}T=\frac{1}{12}.2=\frac{1}{6}s\)
\(S=\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\right).10=\left(\sqrt{3}-1\right).5\)
Tốc độ trung bình: \(v=\frac{S}{t}=\left(\sqrt{3}-1\right).30=21,96\)(cm/s)

Chọn đáp án C
W d = 3 W t ⇒ x = ± A 2
W d = W t ⇒ x = ± A 2
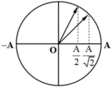
Do xét thời gian ngắn nhất nên ta có thể xét trường hợp như hình vẽ
⇒ v ¯ = S t = A 2 − A 2 T 24 = 24 , 85 c m / s .


Thời gian ngắn nhất cần tìm là thời gian chất điểm đi từ 
hoặc 
Quãng đường cần tìm là :


Chọn A
+ Wđ = 3 Wt => W = Wđ +Wt = 4Wt =>
![]()
+ Tương tự,
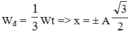
+ Thời gian ngắn nhất là khi vật đi thẳng từ
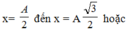
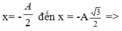
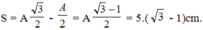
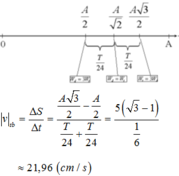
Sử dụng thang thời gian : 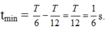
+ Tốc độ trung bình: vtb = S : tmin = 30.(√3 - 1) ≈ 21,96 cm/s.

\(T/4=0,15 \Rightarrow T=0,6s\)
Áp dụng định luật bảo toàn năng lượng từ thời điểm khảo sát cho đến thời gian t:
\( W_đ+W_t = 3W_đ + \dfrac{W_t}{3} \Rightarrow \dfrac{2}{3}.W_t=2W_đ \Rightarrow W_t=3W_đ
\)\(\Rightarrow x_1=A.\dfrac{\sqrt{3}}{2} \Rightarrow x_2=\dfrac{A}{2}
\)
Suy ra thời gian chuyển động từ \(x_1\) đến \(x_2\) là \(\dfrac{T}{12}\)
\(\Rightarrow v_{tb}=\frac{S}{T/12}=73,2cm\)
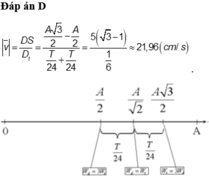

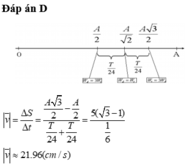

Đáp án D
Các vị trí động năng bằng 3 lần thế năng và bằng một phần ba lần thế năng tương ứng x 1 = ± A 2 x 2 = ± 3 2 A
→ Biễu diễn dao động của vật tương ứng trên đường tròn
+ Tốc độ trung bình của vật v t b = S t = 3 2 A − A 2 T 6 − T 12 = 21 , 96 cm/s