Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi qua VTCB, vận tốc của vật đạt cực đại \(\Rightarrow v_{max} = \omega A = \frac{2\pi}{T} A = 2 (cm/s)\)

Chọn đáp án A
Vận tốc của chất điểm tại vị trí cân bằng có độ lớn v max = ω A = 2 π T A = 8 ( c m / s )

Đáp án C
Vận tốc của vật tại VTCB:
v 0 = A ϖ = A . 2 π T = 1 . 2 . 3 , 14 3 , 14 = 2 m / s

Đáp án A
Vận tốc của chất điểm tại vị trí cân bằng có độ lớn
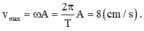 .
.

+ Khi \(W_đ=3W_t\Rightarrow W=4W_t\Rightarrow x=\pm\frac{A}{2}\)
+ Khi \(W_đ=\frac{1}{3}W_t\Rightarrow W=\frac{4}{3}W_t\Rightarrow x=\pm\frac{\sqrt{3}}{2}A\)
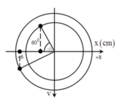
Ta có véc tơ quay như sau:
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(t=\frac{30}{360}T=\frac{1}{12}.2=\frac{1}{6}s\)
\(S=\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\right).10=\left(\sqrt{3}-1\right).5\)
Tốc độ trung bình: \(v=\frac{S}{t}=\left(\sqrt{3}-1\right).30=21,96\)(cm/s)

 Đáp án B
Đáp án B
+ Từ phương trình

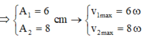
+ Biểu diễn tương ứng hai dao động vuông pha trên đường tròn.
=> Từ hình vẽ, ta có

![]()
+ Dao động thứ hai chậm pha hơn dao động thứ nhất một góc 90 o
=>từ hình vẽ, ta có
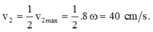
![]()

Tốc độ của vật khi qua vị trí cân bằng v = vmax = ωA = 2 m/s
Đáp án B