

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




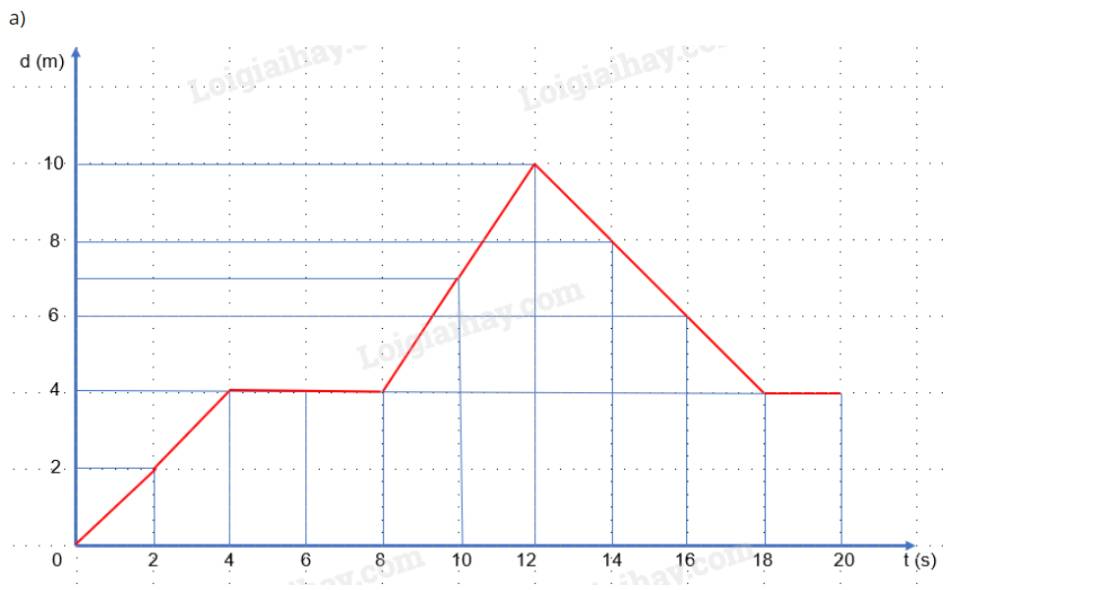
a) Vẽ đồ thị:
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)

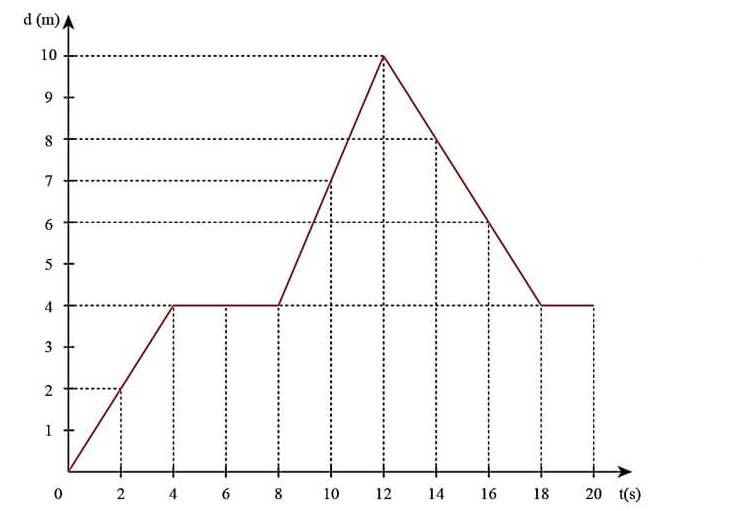
a) Gia tốc của người này tại các thời điểm là:
+ t = 1 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{2}{1} = 2(m/{s^2})\)
+ t = 2,5 s: \(a = 0 (m/{s^2})\)
+ t = 3,5 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{3-4}{{3,5-3}}=-2(m/{s^2})\)
b)
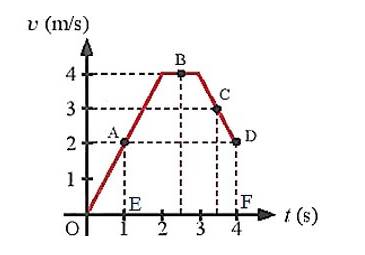
Độ dịch chuyển = Diện tích hình thang OGBE + Diện tích hình thang BKDH + Diện tích hình chữ nhật HDFE
=> Độ dịch chuyển của người này là:
\(\begin{array}{l}d = \frac{1}{2}.(BG + OE).BE + \frac{1}{2}.(BK + HD).BH\ + (EF.DF)\ = \frac{1}{2}.(0,5 + 2,5).4 + \frac{1}{2}.(0,5 + 1,5).2 + 2.1,5 = 11(m)\end{array}\)

a) Gia tốc trên đoạn OA: a 1 = Δ v Δ t = 6 1 = 6 m/s2.
Trên đoạn AB chất điểm chuyển động thẳng đều nên gia tốc a 2 = 0 .
b) Quãng đường chất điểm đi trong 1s đầu tiên: s 1 = 1 2 a 1 t 1 2 = 1 2 .6.1 2 = 3 m.
Quãng đường chất điểm đi trong 2s kế tiếp: s 2 = v t 2 = 6.2 = 12 m.
Quãng đường chất điểm đi trong 3s đầu tiên: s 2 = v t 2 = 6.2 = 12 m.
c) Thời điểm mà chất điểm có vận tốc 2,4m/s: t = v a = 2 , 4 6 = 0 , 4 s.

a,ta có gốc A chiều + AB => X1=Xo+Vot+1/2at^2 vs Xo=0; Vo=10 ;a=-0.2(chậm dần)
=>X1=10t-0.1t^2
xe2 ở B có Xo=560 ,Vo=0 ,a=0.4 => X2=560-0.2t^2 ( xe 2 đi ngược lại B>A )
b,2 xe gặp nhau khi X1=X2 <=> 10t-0.1t^2=560-0.2t^2 <=> t=40(n) t=-140(l)
S1=Vot+1/2at^2=10*40 -0.1*40^2=240
S2=Vot+1/2at^2=0.2*40^2=320
c,tại thời điểm 2 xe gặp nhau t=40 => v xe1 lúc gặp nhau ;V1=Vo-at=10-0.2*40=2
V2=Vo +at=0.4*40=16
vẽ trục oy là v; ox là t trên oy lấy các điểm 2,10,16 trên ox lấy điểm 40 . vẽ đt x1 từ 10 đến giao điểm của 2 vs 40 . vẽ x2 từ 0 đến giao 16 vs 40

1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
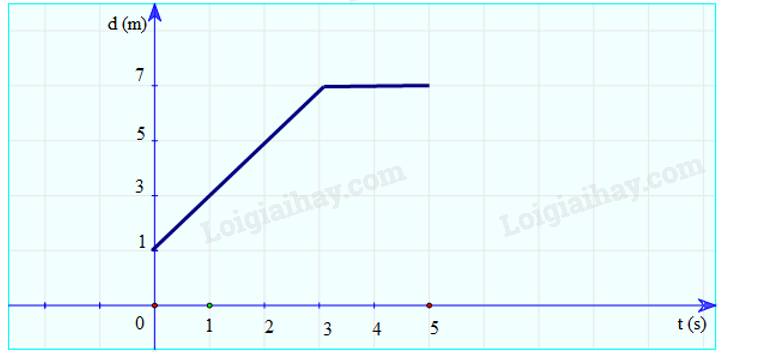
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.

9. Trên một đường thẳng, tại hai điểm A và B cách nhau 10 km, có hai ô tô xuất phát cùng lúc và chuyển động cùng chiều. Ô tô xuất phát từ A có tốc độ 60 km/h và ô tô xuất phát từ B có tốc độ 40 km/h.
a) Lấy gốc tọa độ ở A, gốc thời gian là lúc xuất phát, hãy viết công thức tính quãng đường đi được và phương trình chuyển động của hai xe.
b) Vẽ đồ thị tọa độ - thời gian của hai xe trên cùng một hệ trục (x, t).
c) Dựa vào đồ thị tọa độ - thời gian để xác định vị trí và thời điểm mà xe A đuổi kịp xe B.
Trả lời:
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị
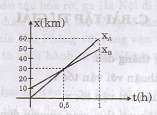
c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị

c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.