Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có ∆l = mg/k = 0,025 m = 2,5 cm.
![]()
![]()
![]()
→ quãng thời gian ![]() ngược chiều nhau là T/6 →
ngược chiều nhau là T/6 →
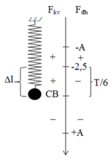 vật
vật
đi từ vị trí π/2 đến 2π/3 và -2π/3 đến –π/2.
→ -A/2 = 2,5 cm.
→ A = 5 cm.

Đáp án B
Tần số góc của dao động ω = k m = 10 rad/s → T = 0,2 s.
→ Tốc độ của vật khi đi qua vị trí cân bằng v = v m a x = ω A = 20 3 cm/s.
+ Dưới tác dụng của ngoại lực con lắc dao động quanh vị trí cân bằng mới O′, tại vị trí này lò xo giãn một đoạn O O ' = Δ l 0 = F k = 2 100 = 2 cm.
+ Tại ví trí xuất hiện ngoại lực, con lắc có x ' = - 2 cm, v ' = v m a x
→ Biên độ dao động của con lắc lúc này A 1 = x ' 2 + v ' ω = 2 2 + 20 3 10 2 = 4 cm.
+ Ta chú ý rằng con lắc dao động quanh vị trí cân bằng mới O′ trong khoảng thời gian Δ t = T 6 = 1 30 s, sau khoảng thời gian này, vật có x 1 = 0 , 5 A 1 , v 1 = 3 v 1 m a x 2 = 3 ω A 1 2 = 3 10 π .4 2 = 20 3 π cm/s.
→ Ngừng lực tác dụng F, con lắc lại dao động quanh vị trí cân bằng cũ, lúc này con lắc có x ′ = O O ′ + 0 , 5 A 1 = 4 c m , v ' = v 1 = 20 3 π cm/s.
→ Biên độ dao động mới A 2 = x ' 2 + v ' ω 2 = 4 2 + 20 3 π 10 π 2 = 2 7 cm.
→ Vậy A 1 A 2 = 4 2 7 = 2 7

Đáp án B
Fdhmax = k(∆l + A) → Fdhmax = mω2(∆l + ∆l)
↔ Fdhmax = 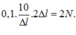

Đáp án C
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 2.10 80 = 2 , 5 cm.
Kéo vật đến vị trí lò xo dãn 7,5 cm rồi thả nhẹ → vật sẽ dao động với biên độ A = 5 cm → E = 0 , 5 k A 2 = 0 , 1 J .
Lực đàn hồi của lò xo có độ lớn nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, nếu chọn chiều dương hướng xuống vị trí này ứng với x = − 2 , 5 cm → E d = 1 2 k A 2 − x 2 = 1 2 80 0 , 05 2 − 0 , 025 2 = 0 , 075 J.
→ Thế năng của vật tại vị trí này là E t = E – E d = 0 , 1 – 0 , 075 = 0 , 025 J .
Lưu ý rằng thế năng của vật bằng tổng thế năng đàn hồi và thế năng trọng trường.
→ Thế năng đàn hồi của vật là E d h = 0 , 025 − 0 , 2.10.0 , 025 = − 0 , 025 J.

Chọn A
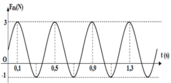
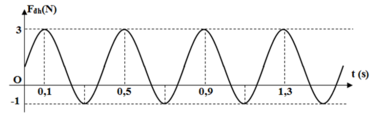
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
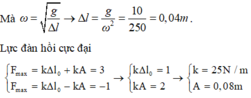
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.

Đáp án D
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
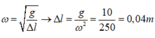
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 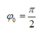 rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm

Đáp án D
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
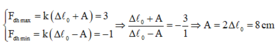
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
![]()
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
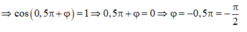
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )

Đáp án C
Độ biến dạng của lò xo tại vị trí cân bằng
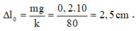
Kéo vật đến vị trí lò xo giãn 7,5 cm rồi thả nhẹ → vật sẽ dao động với biên độ A=5cm.
→ Lực đàn hồi có độ lớn nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng.
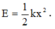
Thế năng của con lắc bằng tổng thế năng đàn hồi và thế năng hấp dẫn. Với gốc thế năng tại vị trí cân bằng thì .
→ Thế năng đàn hồi khi đó có độ lớn
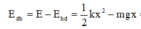
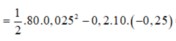
=-0,025J
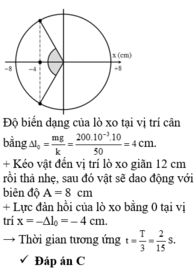
+ Tại vị trí lực đàn hồi của lò xo bằng 12 N ta có:
F d h = m g + k x → k x = 12 − 1.10 = 2 = F k v với x chính là biên độ dao động của vật.
+ Mặc khác: k . Δ l = m g = 10 > k A
® Δ l > A
® Lực đàn hồi nhỏ nhất tác dụng lên vật là: F d h min = k Δ l − A = k Δ l − k A = 10 − 2 = 8 N
Đáp án C