Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biên độ dao động của vật và chiều dài của lò xo khi chưa biến dạng.
A = ( l 1 - l 2 )/2 = (24 - 20)/2 = 2cm
l 0 = l 1 + A = 20 + 2 = 22cm

Tính vận tốc và gia tốc của vật khi đi qua vị trí cân bằng.
Tại vị trí cân bằng vật đạt vận tốc cực đại và gia tốc bằng 0 nên ta có
v = A. ω = 2.5 π = 10 π cm/s
a = 0

Đáp án A
Biên độ dao động của con lắc A = l m a x − l min 2 = 30 − 22 2 = 4 cm
→ Động năng của con lắc tại vị trí có li độ x
E d = E − E t = 1 2 k A 2 − x 2 = 1 2 .100. 0 , 04 2 − 0 , 03 2 = 0 , 035 J

Biên độ dao động của con lắc
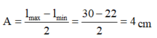
Động năng của con lắc tại vị trí có li độ
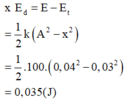
Đáp án A

Đáp án D
Phương pháp: Áp dụng định luật bảo toàn cơ năng
Cách giải:
Biên độ dao động của con lắc lò xo:
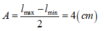
Khi vật cách vị trí biên 4cm tức là vật đang ở li độ x = ± 1 cm
Động năng của vật là:
![]()
= 0,075 J

Biên độ dao động của con lắc là
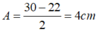
Áp dụng định luật bảo toàn năng lượng ta có
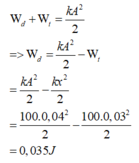
Đáp án D

Con lắc lò xo nằm ngang → Khi lò xo dãn 2 cm, li độ vật có độ lớn x = 2 c m
→ v = ω A 2 - x 2 = 20 π 3 cm / s . Chọn C.

+ Thế năng của con lắc ở vị trí biên:
= 1 2 k x 2 = 1 2 m ω 2 x 2 = 1 2 .0 , 1 4 π 2 . 0 , 1 2 = 0 , 079 J = 79 m J
Chọn đáp án C
Viết phương trình dao động của vật, biết rằng khi t = 0 vật ở vị trí biên x = +A.
Tại thời điểm t =0
A = Acos φ ⇒ cos φ = 1 ⇒ φ = 0
x = Acos2 π ft ⇒ x = 2cos5 π t (cm)