Gọi chiều cao của tòa tháp là h \(\left(m,h>0\right)\)

Chiều cao của tòa tháp là: 

\(\frac{13,1}{0,1}=\frac{h}{2}\Rightarrow h=\frac{13,1\times2}{0,1}=262\left(m\right)\)(TM)

Vậy chiều cao của toà tháp là \(262m\)

Thể tích của kim tự tháp là: \(\frac{1}{3}{.34^2}.21,3 = 8207,6\) (\({m^3}\))

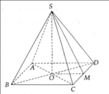
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.

Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.

Tính được:

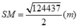
Diện tích xung quanh của kim tự tháp là:

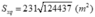
Thể tích của kim tự tháp:

V = 2436819 (m³)

Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.

1. **Tính cạnh bên**:
   Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.

   Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:

   \[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]

   \[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]

   \[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]

   \[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]

   \[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]

2. **Tính diện tích một mặt bên**:
   Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:

   \[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]

   Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:

   \[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]

   \[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]

   \[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]

Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).

Một người đi từ Hà Nội đến Hải Phòng với vận tốc = 40km/h cùng lúc đó một người khác đi từ Hải Phòng về Hà Nội với vận tốc = 50km/h 

Hỏi : a, Sau bao lâu 2 người gặp nhau biết Hà Nội cách Hải Phòng 240km

b, Sau bao lâu 2 người cách nhau 50km ( khi 2 người chưa gặp nhau)

                                               Giải

Giải

A) gọi x là thời gian quãng đường từ Hà Nội ->Hải Phòng; Hải Phòng đi Hà Nội. (ĐK x khác 0; x < 240

Vận tốc của người đó từ Hà Nội đến Hải Phòng là 40 km/h. từ Hải Phòng về Hà Nội là 50 km/h

Quãng đường là 240 km nên ta có phương trình:

                  X+40+50=240

                  X+40=240-50

                  40*x =190

                         X=190/40

                          X=4.75            (TMĐK)

Thời ghian mỗi người cach 50 km là

240/(4.75*50)=1,01 (h)

Vậy a) 4,75 h

       b)1.01 h