Ta có :

\(+\) loại 1 : \(\text{1,7kWh}\)

Số kWh tiêu thụ trong 10 năm của loại 1 là : \(\text{1,7.10 = 17 kWh}\)

1kWh giá 2 500đ \(\Rightarrow\) 17kWh giá 42 500đ

Số tiền chi phí sử dụng tủ lạnh loại 1 kể cả giá tiền tủ lạnh là : \(42500+2500000=2542500\left(đ\right)\)

\(+\) loại 2 : \(\text{1,5kWh}\)

Số kWh tiêu thụ trong 10 năm của loại 2 là : \(\text{1,5.10 = 15 kWh}\)

1kWh giá 2 500đ \(\Rightarrow\) 15kWh giá 37 500đ

Số tiền chi phí sử dụng tủ lạnh loại 2 kể cả giá tiền tủ lạnh là : 

\(3000000+37500=3037500\left(đ\right)\)

\(\Rightarrow\) \(2542500đ\left(loai1\right)< 3037500đ\left(loai2\right)\)

\(\Rightarrow\) Vậy ông A nên mua tủ lạnh loại 1 để tiết kiệm chi phí

Chọn A

Gọi x; y lần lượt là số xe loại M, loại F cần thuê

Từ bài toán ta được hệ bất phương trình

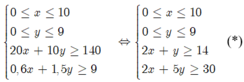
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)

Bài toán trở thành  là tìm x; y nguyên không âm thoả mãn hệ (*)  sao cho T( ;xy)  nhỏ nhất.

Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Tham khảo:

a)

Bước 1: Ta có:

Bước 2: Lập hệ bất phương trình

Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)

Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)

4 tỉ đồng=4000 (triệu đồng)

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình

\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)

Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).

Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)

Bước 3: Xác định miền nghiệm

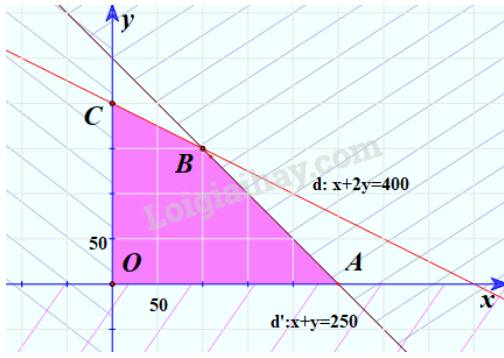
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)

b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)

c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)

Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625

F(100;150)=2,5.100+4.150=850

F(0;200)=2,5.0+4.200=800

Giá trị lớn nhất là F(100;150)=850.

Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.

a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) .

Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250

Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.

Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)

Ta xác định miền nghiệm của hệ bất phương trình trên:

+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).

+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).

+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.

- Vẽ đường thẳng d: x + y = 250.

- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250

Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.

+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.

- Vẽ đường thẳng d’: x + 2y  = 400.

- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400

Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.

Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)

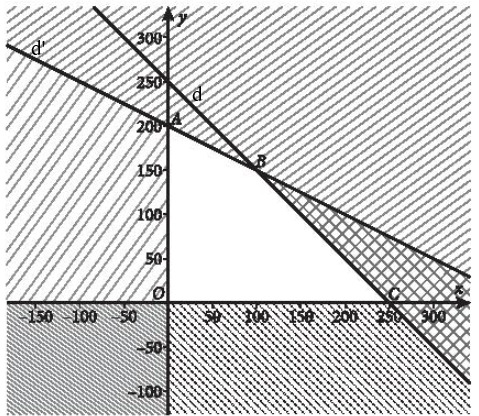
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).

Vậy F(x;y) = 2,5x + 4y.

c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)

Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.

Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;

Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;

Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;

Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.

Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.

Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

Công ty A: \({y_A} = 3750 + 5.x\)(nghìn đồng)

Công ty B: \({y_B} = 2500 + 7,5.x\)(nghìn đồng)

Với \(550 \le x \le 600\)

Ta có:

\(\begin{array}{l}{y_A} - {y_B}=\left( {3750 + 5.x} \right) - \left( {2500 + 7,5x} \right)\\ = 1250 - 2,5x\end{array}\)

Mà \(550 \le x \le 600\)\( \Leftrightarrow 2,5.550 \le 2,5x \le 2,5.600\)

\(\begin{array}{l} \Leftrightarrow 1250 - 1370 \ge 1250 - 2,5x \ge  - 250\\ \Leftrightarrow  - 250 \le 1250 - 2,5x \le  - 120\\ \Rightarrow {y_A} - {y_B} < 0\end{array}\)

Vậy chi phí thuê xe công ty A thấp hơn.

- Gọi số xe loại A và loại B cần dùng là x và y xe .

=> Số tiền là : \(T=4x+3y\)

Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)

Ta có :

- Theo đồ thị thấy cần 5 xe A và 4 xe B nha