Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Phương trình dao động của hai vật:
x1 = A1 cos(ω1t - π/2)
x2 = A2 cos(ω2t - π/2)
+ Hai vật gặp nhau lần đầu khi pha của chúng đối nhau: ω1t - π/2 = - (ω2t - π/2)
=> (ω1 + ω2 ).t = π => t = 2s.

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

Biên độ dao động của vật: \(A=\dfrac{L}{2}=\dfrac{12}{2}=6cm\)
Tần số góc: \(\omega=2\pi f=2\pi\cdot2=4\pi\left(rad\right)\)
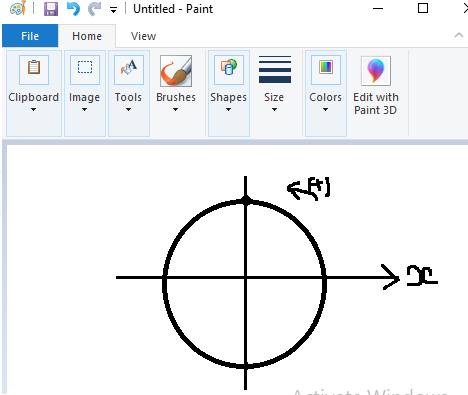
Mốc thời gian lúc vật qua VTCB ngược chiều dương nên \(\varphi_0=\dfrac{\pi}{2}\) (biểu diễn hình như dưới).
Vậy pt dao động là: \(x=Acos\left(\omega t+\varphi_0\right)=6cos\left(4\pi t+\dfrac{\pi}{2}\right)\)

Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động̣ điều hoà
Cách giải :
Biên độ dao động : A = 8cm
Tần số góc:
![]()
Gốc thời gian làlúc vâṭqua VTCB theo chiều âm : φ = π 2
=>. Phương trình dao động: x = 8cos(10 π t + π/2) cm.
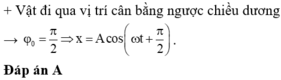



Chu kì dao động: \(T=2\pi/\omega=\pi/10(s)\)
Trong thời gian \(\pi/10\)s đầu tiên bằng đúng 1 chu kì, nên quãng đường đi được là 4A = 4.6=24 cm.