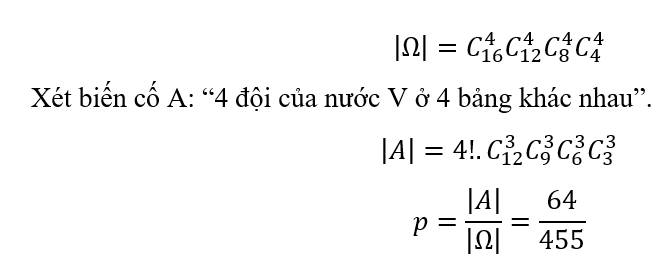a) Ta có: A là tập hợp 32 đội tham gia World Cup 2018.

B là tập hợp 16 đội sau vòng thi đấu bảng (chọn từ 32 đội của tập hợp A sau thi thi đấu theo bảng)

Rõ ràng mỗi phần tử (mỗi đội) của tập hợp B cũng là một phần tử (một đội) của tập hợp A.

Do đó: \(B \subset A\)

Tương tự: Từ 16 đội của B, sau khi đấu loại trực tiếp, còn lại 8 đội vào tứ kết kí hiệu là tập hợp C

Do đó: \(C \subset B\)

Vậy \(C \subset B \subset A\).

b) Tập hợp \(A \cap C\) gồm các đội bóng vừa thuộc 32 đội tham gia World Cup 2018, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.

Tập hợp \(B \cap C\) gồm các đội bóng vừa thuộc 16 đội sau vòng thi đấu bảng, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.

Vậy \(A \cap C = B \cap C = C\)

c) Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các đội thuộc 32 đội tham gia World Cup 2018 nhưng không thuộc 16 đội sau vòng thi đấu bảng.

Vậy đó là 16 đội không vượt qua vòng thi đấu bảng.

Nói cách khác: Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các đội bóng bị loại sau vòng đấu bảng.

Với mỗi bảng, kí hiệu 4 đội lần lượt là A, B, C, D.

Số trận đấu chính là số cách chọn 2 đội thi đấu trong bảng, thực hiện liên tiếp các hoạt động sau:

Chọn một đội thi đấu với đội A: Có 3 cách chọn

Chọn một đội thi đấu với đội B: Có 2 cách chọn

Chọn một đội thi đấu với đội C: Có 1 cách chọn

Vậy sẽ có 3.2.1 = 6 trận đấu trong mỗi bảng.

Vậy 8 bảng có: 8.6 = 48 trận đấu được thi đấu trong vòng bảng

Chú ý:

Thể thức thi đấu vòng tròn một lượt tức là: mỗi đội sẽ lần lượt gặp tất cả các đội khác trong bảng, chỉ đấu 1 lần.

- Mỗi bảng 4 đội thi đấu vòng tròn, giả sử là các đội A, B, C, D

Các trận đấu là: A-B, A-C, A-D, B-C, B-D, C-D => Có tất cả 6 trận đấu

- Có 8 bảng khác nhau.

- Tổng cộng vòng bảng có số trận đấu là 6.8 = 48 (trận đấu).

Số bàn thắng ghi được trong mùa giải đó là:

\(0.5 + 1.10 + 2.5 + 3.3 + 4.2 + 6.1 = 43\) (bàn thắng)

Số bàn thắng trung bình đội đó ghi được trong một trận đấu là:

\(\frac{{43}}{{5 + 10 + 5 + 3 + 2 + 1}} \approx 1,65\)

Vậy trung bình một trận đội đó ghi được 1,65 bàn thắng.

Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.

Số bàn thắng trung bình trong mỗi trận đấu \( = \frac{{6 + 6 + 2 + 1 + 2 + 4 + 3}}{7} = 3,43\)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega  \right) = C_{12}^4\)

a) Số kết quả thuận lợi cho biến cố “Bốn bạn thuộc 4 tổ khác nhau” là số cách sắp xếp 4 bạn vào 4 tổ có \(4!\) cách

Vậy xác suất của biến cố “Bốn bạn thuộc 4 tổ khác nhau” là \(P = \frac{{4!}}{{C_{12}^4}} = \frac{8}{{165}}\)

b) Gọi A là biến cố “Bốn bạn thuộc 2 tổ khác nhau”

A xảy ra với 2 trường hợp sau:

TH1: 3 bạn cùng thuộc 1 tổ và 1 bạn thuộc tổ khác có \(C_4^3.C_3^1.C_2^1 = 24\) cách

TH2: cứ 2 bạn cùng thuộc 1 tổ \(C_4^2.C_3^1.C_2^2.C_2^1 = 36\) cách

Suy ra, số kết quả thuận lợi cho biến cố A là \(n\left( A \right) = 24 + 36 = 60\)

Vậy xác suất của biến cố “Bốn bạn thuộc 2 tổ khác nhau” là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{60}}{{C_{12}^4}} = \frac{4}{{33}}\)

a) Các đội thi đấu vòng tròn một lượt và mỗi lượt đấu sẽ có 2 đội đấu với nhau, nên số trận đấu sẽ là số cách chọn ra 2 đội từ 7 đội, mỗi cách chọn 2 đội từ 7 đội là một tổ hợp chập 2 của 7, từ đó có tất cả số trận đấu là:

\(C_7^2 = \frac{{7!}}{{2!.5!}} = 21\) (trận)

b) Mỗi khả năng ba đội được chọn đi thi đấu cấp liên trường là một tổ hợp chập 3 của 7 đội, từ đó số khả năng có thể xảy ra của 3 đội đi thi cấp liên trường là

                   \(C_7^3 = \frac{{7!}}{{3!.4!}} = 35\)

Đáp án C

Ta xét dự đoán của bạn Dung, giả sử dự đoán B nhì của Dung đúng thì dẫn đến B nhất của Trung là sai do đó D nhì của Trung là đúng (mâu thuẫn giả thiết B nhì)

Như vậy C thứ ba là đúng suy ra A nhì B nhất và D thứ tư.