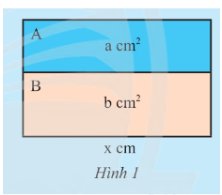
a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)

Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)

Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)

Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)

b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)  

Gọi chiều dài là: x  ( 0 < x < 16 , cm) 

Nửa chu vi là: 32 : 2 = 16  cm 

Chiều rộng là: 16 - x ( cm) 

Diện tích là: x ( 16 - x )  ( cm^2 ) 

Tăng chiều dài lên 3cm => Chiều dài mới là: x + 3 ( cm) 

Giảm chiều rộng xuống 3cm => Chiều rộng  mới là: 16 - x - 3 = 13 - x ( cm) 

Diện tích mới là: ( x + 3 ) ( 13 - x ) ( cm^2) 

Theo bài ra ta có phương trình: x ( 16 - x )  = ( x + 3 ) ( 13 - x ) + 21

<=> 16 x - x^2 =- x^2 + 10x + 60 

<=> x = 10  tm 

Vậy diện tích ban đầu là: x ( 16 - x ) = 10 ( 16 - 10 ) = 60 ( cm^2) 

C.6m

hi mik là fa ruru

Gọi x (m) là chiều rộng (x > 0)

⇒ x + 5 (m) là chiều dài

Chiều rộng sau khi tăng: x + 2 (m)

Chiều dài sau khi giảm: x + 5 - 3 = x + 2 (m)

Diện tích lúc đầu: x(x + 5) = x² + 5x (m²)

Diện tích lúc sau: (x + 2)(x + 2) (m²)

Theo đề bài ta có phương trình:

x² + 5x - 16 = (x + 2)(x + 2)

⇔ x² + 5x - 16 = x² + 2x + 2x + 4

⇔ x² + 5x - x² - 2x - 2x = 4 + 16

⇔ x = 20 (nhận)

Vậy chiều rộng của hình chữ nhật là 20 m

Chiều dài của hình chữ nhật là 20 + 5 = 25 m

Gọi x, y lần lượt là độ dài của chiều dài và chiều rộng (\(0< y< x,x>5\) )

Theo đề, có:

\(\left\{{}\begin{matrix}x-y=5\\\left(x-3\right)\left(y+2\right)=xy-16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-y=5\\2x-3y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=25\\y=20\end{matrix}\right.\) (nhận)

Vậy kích thước lúc đầu của hình chữ nhật là: \(x.y=25.20=500\left(m^2\right)\)