
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

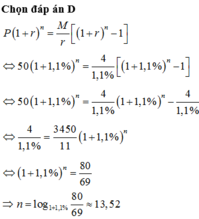

Chọn D
Vay vốn trả góp: Vay ngân hàng số tiền là P đồng với lãi suất r% trên tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi tháng hoàn nợ số tiền là X đồng và trả hết số tiền nợ sau đúng n tháng



Tổng số tiền còn nợ ngân hàng sau tháng thứ 1 là ![]()
Tổng số tiền còn nợ ngân hàng sau tháng thứ 2 là
![]()
![]()
Tổng số tiền còn nợ ngân hàng sau tháng thứ n là
![]()
![]()
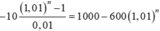
Trước tiên giải ![]()
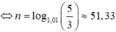
Số tiền còn nợ ngân hàng sau tháng thứ 51 là ![]() đồng.
đồng.
Số tiền phải trả cho ngân hàng cho tháng thứ 52 (kỳ cuối cùng) là
![]() đồng.
đồng.
Chọn đáp án B.

Đáp án A
Gọi T là số tiền B đã vay, r là lãi suất
Ta có:
Số tiền còn nợ sau 1 tháng là:
T 1 + r − m 1 = 1 , 01 T − 10 (với m i là số tiền mà bạn B trả tháng thứ i)
Số tiền còn nợ sau 2 tháng là:
1 , 01 T − 10 1 + r − 20 = 1 , 01 T − 10 .1 , 01 − 20 = 1 , 01 2 T − 30 , 1
Số tiền còn nợ sau 3 tháng là:
1 , 01 2 T − 30 , 1 1 + r − 30 = 1 , 01 2 T − 30 , 1 .1 , 01 − 30 = 1 , 01 3 T − 60 , 401
Cho 1 , 01 3 T − 60 , 401 = 0 ⇔ T = 58 , 62 triệu đồng.

Đáp án D
Tổng quát:
Giả sử người đó vay ngân hàng số tiền A triệu đồng.
Lãi suất: r % / tháng.
Cuối mỗi tháng người đó trả a triệu đồng.
Cuối tháng đầu tiên, số tiền A triệu đồng ban đầu sinh ra cả gốc lẫn lãi là A + Ar = A 1 + r . Sau khi trả a triệu đồng thì người đó còn nợ A 1 + r − a .
Cuối tháng thứ hai, sau khi trả a triệu đồng người đó còn nợ A 1 + r − a 1 + r − a .
= A 1 + r 2 − a 1 + r − a
…
Cuối tháng thứ n, sau khi trả a triệu đồng người đó còn nợ
A 1 + r n − a 1 + r n − 1 − . .. − a = A 1 + r n − a [ 1 + r n − 1 + 1 + r n − 2 . .. + 1 ]
= A 1 + r n − a . 1 + r n − 1 r
Giả sử đến cuối tháng thứ n thì người đó trả hết nợ, khi đó
A 1 + r n − a . 1 + r n − 1 r = 0
⇔ A 1 + r n = a r 1 + r n − 1 ⇔ 1 + r n a r − A = a r .
Thay số:
n = log 1 + 0 , 6 100 10 10 − 200 . 0 , 6 100 ≈ 21 , 37
Vậy sau ít nhất 22 tháng thì người đó trả được hết số nợ ngân hàng.