Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn vẽ hình ra giúp mình nha.
Đổi 72km/h=20m/s
a, Ta có: \(v^2-v_0^2=2aS\)
\(\Leftrightarrow0-\left(20\right)^2=2.a.500\)
\(\Leftrightarrow a=-0,4\left(\dfrac{m}{s^2}\right)\)
Lực hãm phanh: Fhãm=-ma=-2.104.(-0,4)=8000(N)
b, Thời gian từ lúc ô tô hãm phanh tới lúc dừng hẳn là:
v=v0+at \(\Leftrightarrow0=20-0,4t\Leftrightarrow t=50\left(s\right)\)
Bạn tham khảo nha
Tôi k hỉu chỗ : -2.10 mũ 4 . (-0.4) ( giải thích hộ tôi với chứ tôi nghĩ là lấy 2000*-0.4 thôi

Đổi 2 tấn = 2000 kg
36 km/h = 10 m/s
a. Gia tốc của xe là:
\(a=\dfrac{\Delta v}{t}=\dfrac{0-10}{2}=-5\) (m/s)
Độ lớn của lực hãm là:
\(\left|F\right|=\left|ma\right|=10000\) (N)
Hệ số ma sát giữa xe với mặt đường là:
\(\mu=\dfrac{F}{N}=\dfrac{10000}{20000}=0,5\)
b. Quãng đường xe đi được cho đến khi dừng lại là:
\(s=\dfrac{v^2}{2a}=\dfrac{10^2}{2.5}=10\) (m)

Đổi 3 tấn =3000 kg
Độ lớn của v0 là
\(s=v_0t+\dfrac{1}{2}at^2\Rightarrow15=3v_0+\dfrac{9}{2}a\) (1)
\(v^2-v_0^2=2as\Rightarrow-v_0^2=30a\) (2)
Từ (1) và (2) \(\Rightarrow v_0=\dfrac{100}{19}\left(\dfrac{m}{s}\right);a=-\dfrac{10}{57}\left(\dfrac{m}{s^2}\right)\)
Độ lớn lực hãm phanh
\(a=\dfrac{F}{m}\Rightarrow F=a\cdot m=\dfrac{10}{57}\cdot3000\approx526,31\left(N\right)\)

Ta có: \(v^2-v_0^2=2as\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2s}=\dfrac{0^2-10^2}{2\cdot50}=-1\left(m/s^2\right)\)
Quãng đường mà vật di chuyển trong 4s kể từ lúc hãm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2\)
\(\Rightarrow s=10\cdot4+\dfrac{1}{2}\cdot-1\cdot4^2=32\left(m\right)\)

\(v_0=72\)km/h=20m/s
\(v=0\)m/s
Gia tốc vật: \(v^2-v^2_0=2aS\)
\(\Rightarrow a=\dfrac{v^2-v^2_0}{2S}=\dfrac{0-20^2}{2\cdot10}=-20\)m/s2
Lực cản:
\(F_c=m\cdot a=5000\cdot\left(-20\right)=-10^5N\)

Chọn đáp án B
1 2 m v 2 = F . s ⇒ F = m v 2 2 s = 1500 . 15 2 . 50 2 = 3375 ( N )

Chọn đáp án A
? Lời giải:
+ v 2 − v 0 2 = 2as, với: v0 = 79,2 km/giờ = 22 m/s, v = 0, s = 100 m
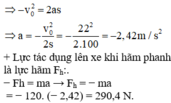
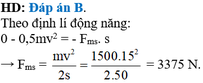
a. Ta có: \(\left\{{}\begin{matrix}s=v_0t+\dfrac{1}{2}at^2\Leftrightarrow24=v_0\cdot4+\dfrac{1}{2}\cdot a\cdot4^2\Leftrightarrow24=v_0\cdot4+8a_{\left(1\right)}\\v_0+at=0\Leftrightarrow v_0=-a\cdot4_{\left(2\right)}\end{matrix}\right.\)
Thay (2) vào (1): \(24=8a-16a\)
\(\Rightarrow a=-3\left(\dfrac{m}{s^2}\right)\)
\(\Rightarrow v_0=-at=-3\cdot-4=12\left(\dfrac{m}{s}\right)\)
b. \(F_{ham}=ma=2000\cdot-3=-6000\left(N\right)\)
c. \(F'_{ham}=3F_{ham}=3\cdot-6000=-18000\left(N\right)\)
\(F'_{ham}=ma'\Rightarrow a'=\dfrac{F'_{ham}}{m}=\dfrac{-18000}{2000}=-9\left(\dfrac{m}{s^2}\right)\)
\(v^2-v_0^2=2a'S'\)
\(\Leftrightarrow0^2-12^2=2\cdot-9\cdot S'\)
\(\Leftrightarrow-144=-18\cdot S'\)
\(\Rightarrow S'=8\left(m\right)\)