Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
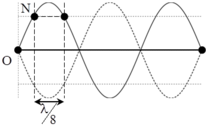
+ Bước sóng của sóng l = 3 λ 2 ⇒ λ = 2 3 l = 60 cm
+ Điểm N dao động với biên độ A N = 2 2 = 2 2 A o ⇒ N
các bụng gần nhất một đoạn λ 8
+ Trên cả sợi dây A N = λ 8 + k λ 4 = 7 , 5 + 15 k
Ta dễ dàng kiểm tra được giá trị 50,5 là không phù hợp
Đáp án B
Đáp án C
+ Khi xuất hiện sóng dừng, trên dây có hai bụng sóng → sóng dừng trên dây với hai bó sóng → λ = 24cm → M và N lần lượt cách nút gần nhất một đoạn λ/6 = 4 cm.
A N = A M = A b 3 2 = 2 3 3 2 = 3 cm .
+ M và N thuộc hai bó sóng liên tiếp nên dao động ngược pha nhau → MN lớn nhất khi M và N cùng đến biên, MN nhỏ nhất khi M và N cùng đến biên, MN nhỏ nhất khi M, N cùng đi qua vị trí cân bằng.
→ σ = MN 2 + ( 2 A N ) 2 MN 2 = 8 2 + 6 2 8 2 = 1 , 25 .
Đáp án C
+ A, B là nút sóng, trên dây AB có bụng sóng ⇒ λ = l = 24 c m
+ M, N là hai điểm trên dây chia thành 3 đoạn bằng nhau khi dây duỗi thẳng → M, N cách nút sóng gần đó nhất đoạn λ 6 = 4 c m
⇒ A M = A N = A b sin 2 π . λ 6 λ = 3 c m
+ M, N thuộc hai bó liên tiếp nhau nên dao động ngược pha với nhau.
+ Khoảng cách MN nhỏ nhất khi sợi dây duỗi thẳng M N min = A B 3 = 8 c m
+ Khoảng cách MN lớn nhất khi M, N cùng đến biên:
M N max = A B 3 2 + A M + A M 2 = 10 c m
+ Vậy δ = M N max M N min = 10 8 = 1 , 25
Đáp án A
+ Khi xảy ra sóng dừng trên dây có 20 bụng sóng
+ Biên độ dao động của các phần tử dây cách nút A một đoạn d được xác định bằng biểu thức:
với 
là biên độ của điểm bụng
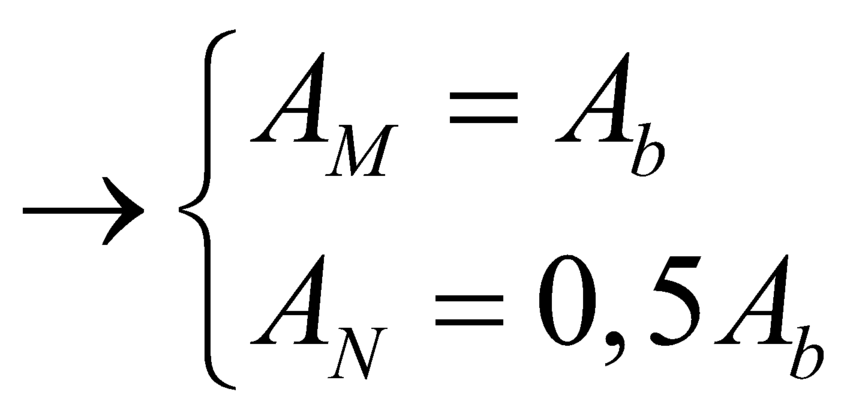
+ Theo giả thuyết của bài toán
Đáp án A
+ Khi xảy ra sóng dừng trên dây có 20 bụng sóng
+ Biên độ dao động của các phần tử dây cách nút A một đoạn d được xác định bằng biểu thức:
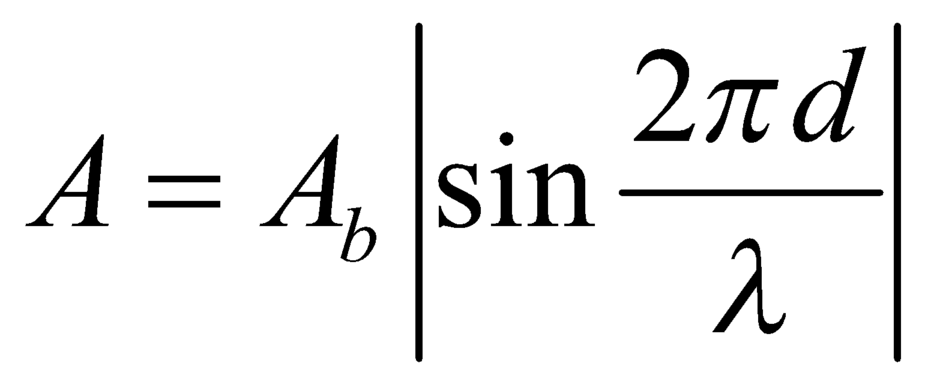
với 
là biên độ của điểm bụng
+ Theo giả thuyết của bài toán
