Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng: \(a = -\omega^2 x =-(2\pi)^2.3 = - 120\ cm/s^2 \)

Để tính vị trí của vật điều hoà tại thời điểm 1/3 giây sau khi vật có li độ x = 3cm, chúng ta cần tính giá trị của x tại thời điểm đó.
Phương trình vật dao động điều hoà đã cho là: x = 6cos(2πt - π/6) (cm)
Để tìm thời điểm 1/3s tiếp theo, ta thay t = 1/3 vào phương trình trên:
x = 6cos(2π(1/3) - π/6) = 6cos(2π/3 - π/6) = 6cos(π/2) = 6 * 0 = 0 (cm)
Vậy, tại thời điểm 1/3s tiếp theo, vật sẽ ở li độ x = 0cm.

Chu kì: \(T=\frac{2\pi}{5\pi}=0,4s\)
Trong thời gian 1/10 s = 1/4 T thì véc tơ quay đã quay một góc: 360/4 = 900.
Biểu diễn bằng véc tơ quay, ta dễ dàng tìm đc li độ thời điểm sau đó 1/10 s là 4 và -4cm.

Gia tốc của vật tại li độ x là a = - ω 2 x = - 120 cm/s2
Đáp án A

a) \(v_{max}=\omega.A\Rightarrow \omega=\dfrac{10\pi}{5}=2\pi(rad/s)\)
Vậy PT dao động là: \(x=5\cos(2\pi t+\dfrac{\pi}{3})cm\)
b) Áp dụng CT độc lập:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 5^2=3^2+\dfrac{v^2}{(2\pi)^2}\)
\(\Rightarrow v=\pm 8\pi(cm/s)\)

\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3

Đáp án C
Phương pháp: Áp dụng hệ thức độc lập với thời gian của li độ và vận tốc
Cách giải:
Áp dụng hệ thức độc lập:
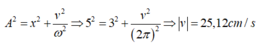

Áp dụng: \(A^2 = x^2 + \frac{v^2}{\omega^2} \Rightarrow v = \pm\omega\sqrt{A^2-x^2}\),
Thay số, ta được v = \(\pm\) 25,12 cm/s.
sai rồi ạ, bạn chưa xem pha ban đầu Pi/3