Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

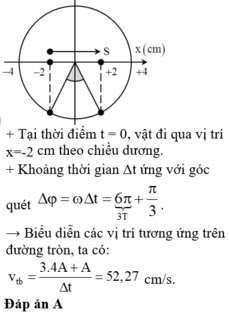
Biểu diễn dao động bằng véc tơ quay, sau 2/3 s thì véc tơ quay đc góc là: \(\alpha=\omega.t=\dfrac{4\pi}{3}\) rad
Ta có:
Ban đầu véc tơ quay xuất phát ở M, sau đó nó quay đến N.
Quãng đường vật đi là: \(\dfrac{A}{2}+2A=\dfrac{5A}{2}\)
Suy ra: \(\dfrac{5A}{2}=15\Rightarrow A=6(cm)\)
Tốc độ cực đại: \(v_{max}=\omega.A=2\pi.6=12\pi(cm/s)\)

Để tính quãng đường vật đi được sau 0,25 s, ta có thể sử dụng phương trình dao động điều hòa x = A * cos(2π/T * t + φ), trong đó x là vị trí của vật (cm), A là biên độ của vật (cm), T là chu kỳ của dao động (s), t là thời gian (s), và φ là góc pha ban đầu (rad).
Trong trường hợp này, phương trình dao động là x = 4cos(4πt + π/4). Ta có thể nhận thấy rằng biên độ của vật là 4 cm và chu kỳ của dao động là T = 1/4 s.
Để tính quãng đường vật đi được sau 0,25 s, ta thay t = 0,25 vào phương trình:
x = 4cos(4π * 0,25 + π/4)
x = 4cos(π + π/4)
x = 4cos(5π/4)
x ≈ 4 * (-0,7071)
x ≈ -2,8284 cm
Vậy, quãng đường vật đi được sau 0,25 s kể từ khi bắt đầu chuyển động là khoảng -2,8284 cm.

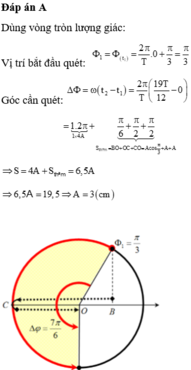
Biểu diễn dao động bằng véc tơ quay:
Ban đầu, véc tơ quay xuất phát ở M, để dao động đi được 6cm thì véc tơ quay sẽ quay đến N.
Trên hình vẽ ta tìm được góc quay là: \(\alpha=90+30=120^0\)
Thời gian: \(t=\dfrac{120}{360}T=\dfrac{\pi}{30}\)
\(\Rightarrow T=\dfrac{\pi}{10} (s)\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Cơ năng của vật: \(W=\dfrac{1}{2}.m.\omega^2.A^2=\dfrac{1}{2}.1.20^2.0,04^2=0,32(J)\)


Biểu diễn dao động bằng véc tơ quay:
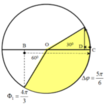
Ban đầu véc tơ quay xuất phát ở M, khi véc tơ quay đến N thì dao động đi từ 6cm --> -3cm.
Khi đó, quãng đường đi được là 9cm.
Góc quay mà véc tơ quay đã quay được là: \(90+30=120^0\)
Thời gian: \(t=\dfrac{120}{360}.T=\dfrac{1}{30}\)
\(\Rightarrow T = \dfrac{1}{10}(s)\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=20\pi (rad/s)\)