Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Động năng biến thiên với chu kì bằng nửa chu kì của li độ dao động.
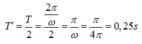

Chọn B
Động năng biến thiên với chu kì bằng nửa chu kì của li độ dao động.
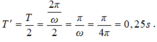

Chọn C
Từ biểu thức tổng quát x = Acos(ωt + φ), ta tìm:
+ A: Quãng đường đi trong 1 chu kỳ là 4A => A = S/4 = 10cm
+ ω: Số dao động trong 1 giây: n = f = N t = 120 60 = 2 ( H z ) => ω = 2πf = 4π rad/s.
+ φ: t = 0 => x = A cosφ = 5; v = -Asinφ < 0 => φ = π/3 rad.
Vậy: x = 10 cos ( 4 πt + π 3 ) cm .

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Đáp án A
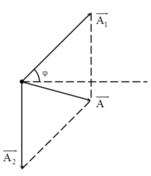
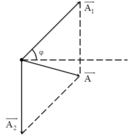
Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
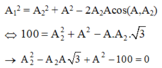
Phương trình trên luôn có nghiệm nên:



C. x = 20cos(4πt + π/3)(cm)