Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

Xem giản đồ Fre-nen (H.5.6G)
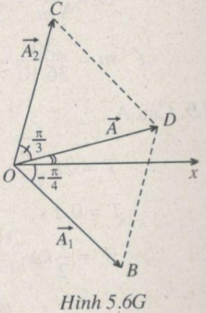
A 1 → + A 2 → = 6cm ⇒ ∆ COD cân
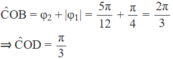
Pha ban đầu của dao động tổng hợp là :
![]()
A → = A 1 → = A 2 →

Vì cos ω t = sin( ω t + π /2) nên dao động của điểm Q trên trục y có thể viết dưới dạng y = Acos ω t. Vì vậy hiệu số pha giữa hai dao động của P và Q bằng 0.
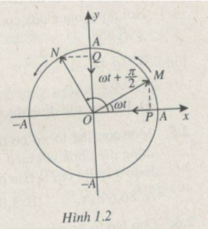

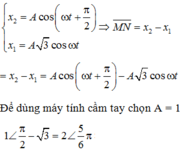
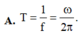
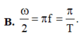
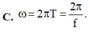
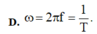
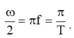
Dao động điều hòa là dao động có toạ độ là một hàm sin hoặc côsin theo thời gian dạng x = Acos( ω t + φ ) hoặc
x = Asin( ω t + φ )
Trong đó chu kì: là khoảng thời gian ngắn nhất để vật lặp lại một trạng thái dao động (trạng thái cũ gồm: vị trí cũ và chiều chuyển động cũ) ⇒ T = ∆ t N = 2 π ω