Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong trường hợp khí cầu đang bay lên thì lúc đầu vật được ném lên cao với vận tốc đầu v 0 = 4,9 m/s bằng vận tốc bay lên của khí cầu từ độ cao s và chuyển động chậm dần đều trong khoảng thời gian t 2 lên tới độ cao lớn nhất, tại đó v = 0. Khoảng thời gian t 2 được tính theo công thức:
v = v 0 – g t 2 = 0 ⇒ t 2 = 0,5 s
Sau đó vật lại rơi tự do từ độ cao lớn nhất xuống đến độ cao 300 m trong thời gian t 2 = 0,5 s, rồi tiếp tục tơi nhanh dần đều với vận tốc v 0 = 4,9 m/s từ độ cao 300 m xuống tới đất trong khoảng thời gian t 1 ≈ 7,3 s (giống như trường hợp trên).
Như vậy, khoảng thời gian chuyển động của vật sẽ bằng: t = 2 t 2 + t 1 = 2.0,5 + 7,3 = 8,3 s.

Trong trường hợp khí cầu đang hạ xuống thì vật rơi nhanh dần đều với vận tốc đầu v 0 = 4,9 m/s bằng vận tốc hạ xuống của khí cầu từ độ cao s được tính theo công thức s = v 0 t + (g t 2 )/2
Thay số vào ta thu được phương trình bậc 2:
300 = 4.9t + (9.8 t 2 )/2 ⇔ t 2 + t - 300/4.9 = 0
Giải ra ta tìm được t ≈ 7,3 s (chú ý chỉ lấy nghiệm t > 0)
Như vậy thời gian rơi của vật là t ≈ 7,3 s

c,
Khi khí cầu đang bay lên thì lúc đầu vật được ném lên cao với vận tốc vo = 4,9 m/s bằng vận tốc bay lên của khí cầu từ độ cao s và chuyển động thẳng chậm dần đều trong khoảng thời gian t2 lên tới độ cao lớn nhất , tại đó v = 0 .
=> khoảng thời gian t2 tính theo công thức
v = vo - gt2 = 0
=> t2 = \(\frac{vo}{g}=\frac{4,9}{9,8}=0,5s\)
Sau đó vật rơi tự do từ độ cao lớn nhất xuống độ cao 300m trong thời gian t2 = 0,5s rồi tiếp tục rơi nhanh dần đều với vận tốc vo = 4,9m/s từ độ cao 300m xuống tới đất trong khoảng thời gian t1 \(\approx7,3s\)
=> khoảng thời gian chuyển động là
t = 2t2 + t1 = 2. 0,5 + 7,3 = 8,3 s
a,
Khi khí cầu đứng yên thì quãng đường vật rơi tự do từ độ cao s theo công thức
s =\(\frac{gt^2}{2}\)
=> khoảng thời gian rơi tự do của vật bằng :
t = \(\sqrt{\frac{2s}{g}}\)
= \(\sqrt{\frac{2.300}{9,8}}\)
\(\approx\) 7,8 ( s )

a, lấy g=10m/s
ta có \(300=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{60}\left(s\right)\)
b, vận tốc đầu của vật là -5m/s
\(300=-5.t+\dfrac{1}{2}gt^2\Rightarrow t\approx8,3\left(s\right)\)
c, vận tốc đầu 5m/s
\(300=5t+\dfrac{1}{2}gt^2\Rightarrow t\approx7,262\left(s\right)\)
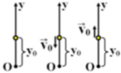
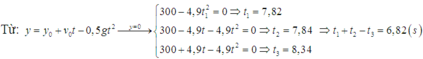
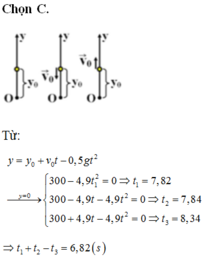

Trong trường hợp khí cầu đứng yên thì quãng đường vật rơi tự do từ độ cao s tính theo công thức s = (g t 2 )/2
Từ đó suy ra khoảng thời gian rơi tự do của vật bằng: t = 2 h g = 2 . 300 9 , 8