Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49 m/s.

a, Phương trình vận tốc là: v(t) = \(3t^2-6t+8\)
Phương trình gia tốc là: a(t) = \(6t-6\)
Thay t = 3 vào phương trình, ta được:
s = \(3^3-3\cdot3^3+8\cdot3+1=25\left(m\right)\)
\(v=3\cdot3^2-6\cdot3+8=17\left(m/s\right)\\ s=6\cdot3-6=12\left(m/s^2\right)\)
b, Theo đề bài, ta có:
\(t^3-3t^2+8t+1=7\\ \Leftrightarrow t^3-3t^2+8t-6=0\\ \Leftrightarrow\left(t-1\right)\left(t^2-2t+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=1\\t^2-2t+6=0\left(vô.nghiệm\right)\end{matrix}\right.\)
Khi t = 1(s), chất điểm đi được 7m
\(v=3\cdot1^2-6\cdot1+8=5\left(m/s\right)\\ a=6\cdot1-6=0\left(m/s^2\right)\)

Phương trình vận tốc của vật là: v(t) = s'(t) = gt
Phương trình gia tốc của vật là: a(t) = v'(t) = g = 9,8 m/s2
a, Vận tốc tại thời điểm t0 = 2(s) = \(9,8\cdot2=19,6\left(m/s\right)\)
b, Gia tốc của vật tại mọi thời điểm là a = g = 9,8 m/s2

a, Phương trình vận tốc v(t) = s'(t) = gt
Vận tốc tức thời tại thời điểm t0 = 4(s) là: \(v\left(4\right)=39,2\left(m/s\right)\)
Vận tốc tức thời tại thời điểm t0 = 4,1s) là: \(v\left(4,1\right)=40,18\left(m/s\right)\)
b, Tỉ số \(\dfrac{\Delta v}{\Delta t}=\dfrac{40,18-39,2}{4,1-4}=9,8\)

a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49
m/s.

Phương trình gia tốc là: \(a\left(t\right)=v'\left(t\right)=2t+2\)
a, Tại thời điểm t = 3(s), gia tốc tức thời là: \(a\left(3\right)=2\cdot3+2=8\left(m/s^2\right)\)
b, Vận tốc của chất điểm bằng 8
\(\Rightarrow t^2+2t-8=0\\ \Leftrightarrow\left(t-2\right)\left(t+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-4\left(loại\right)\end{matrix}\right.\)
Vậy khi t = 8s thì chất điểm đạt vận tốc 8m/s.

Ta có s = 1 2 g t 2 => s ' ( t ) = g . t = v ( t )
Khi đó v ( 5 ) = 9 , 8.5 = 49 m/s
Chọn đáp án A

Gọi k là hệ số góc của tiếp tuyến .
Phương trình tiếp tuyến vuông góc với đường thẳng y = 1 7 x − 4 nên:
k . 1 7 = − 1 ⇒ k = − 7
Với k=-7 ta có f ' x = 3 x 2 − 10 x = − 7 ⇔ 3 x 2 − 10 x + 7 = 0
⇔ x = 1 x = 7 3
Ứng với 2 giá trị của x ta viết được 2 phương trình tiếp tuyến thỏa mãn.
Chọn đáp án B
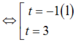
a) Vận tốc trung bình trong khoảng thời gian từ t đến t + Δt là:
b) Vận tốc tức thời tại thời điểm t = 5s chính là vận tốc trung bình trong khoảng thời gian (t; t + Δt) khi Δt → 0 là :