Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a)
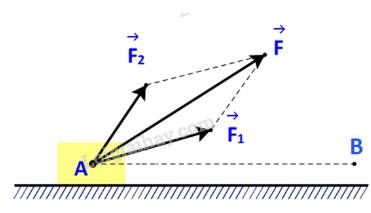
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
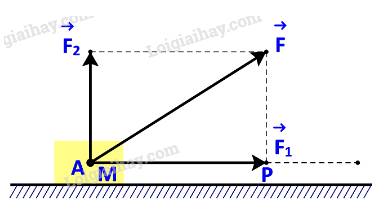
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).

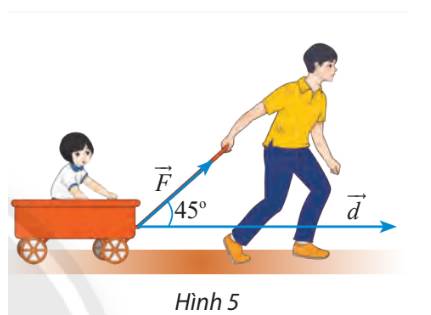
Theo giả thiết ta có: \(A = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right)\)
\( \Rightarrow A = 10.100.\cos 45^\circ = 500\sqrt 2 \left( J \right)\)
Vậy công sinh bởi lực \(\overrightarrow F \) là \(500\sqrt 2 \) (J)

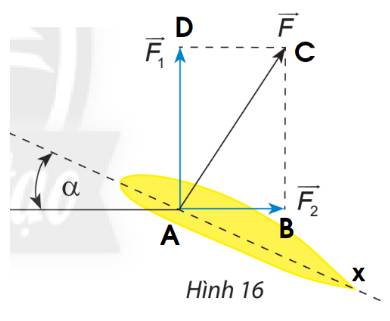
Khi đó các lực \(\overrightarrow F ,\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AB} \)
\(\alpha = \widehat {{\rm{BAx}}} = 30^\circ \) \( \Rightarrow \widehat {CAB} = 60^\circ \)
\(AB = AC.c{\rm{os}}\widehat {CAB} = a.c{\rm{os60}}^\circ {\rm{ = }}\frac{a}{2} \Rightarrow \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AB} } \right| = \frac{a}{2}\)
\(AD = BC = AC.\sin \widehat {CAB} = a.\sin 60^\circ = \frac{{a\sqrt 3 }}{2} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {AD} } \right| = AD = \frac{{a\sqrt 3 }}{2}\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \frac{{a\sqrt 3 }}{2};\left| {\overrightarrow {{F_2}} } \right| = \frac{a}{2}\)


Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N.

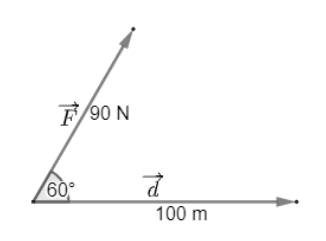
Công sinh bởi lực \(\overrightarrow F \) được tính bằng công thức
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 90.100.\cos 60^\circ = 4500\) (J)
Vậy công sinh bởi lực \(\overrightarrow F \) có độ lớn bằng 4500 (J)

Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}
{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\
\begin{array}{l}
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha
\end{array}\\
{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }
\end{array}\)

Gọi vectơ dịch chuyển của vật là \(\overrightarrow d \), ta có \(|\overrightarrow d |\; = 50\).
Theo giả thiết \(\overrightarrow F \) và \(\overrightarrow d \) cùng hướng nên \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 0^\circ \)
Công sinh ra bởi lực \(\overrightarrow F \)được tính bằng:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 20.50.\cos 0^\circ = 1000\) (J)

Tham khảo:
Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
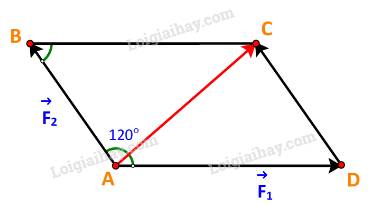
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Xét \(\Delta ABC\) ta có:
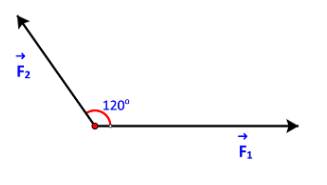
\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)

Tham khảo:
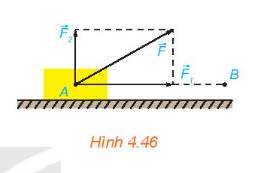
Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)
Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.
\( \Leftrightarrow A\) là trung điểm của EC.
Bước 2:
Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)
Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)
\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)
Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)
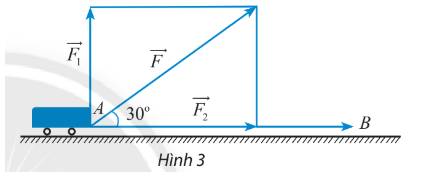

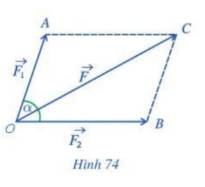

Ta xác định được các độ lớn:
\(\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ = 50.\frac{1}{2} = 25\) (N)
Dựa vào hình vẽ ta có: \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ \)
Áp dụng công thức tính công sinh ra bởi lực \(A = \overrightarrow F .\overrightarrow d \) ta có:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ = 5000 (J)\)
\({A_1} = \overrightarrow {{F_1}} .\overrightarrow d = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ = 0 (J)\)
\({A_2} = \overrightarrow {{F_2}} .\overrightarrow d = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ = 5000\sqrt 3 (J)\)