Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toán C37
Matt là người chạy nhanh thứ 50 nên thứ hạng nằm khoảng từ 1 đến 50
Matt cũng là người chạy chậm thứ 50 nên thứ hạng nằm khoảng 99 đến 50 (Vì từ 50 đến 99 có (99 - 50):1+1=50 số hạng)
Từ 1 đến 99 có (99 - 1):1+1=99 số hạng
Vậy có 99 người tham gia thi chạy

Toán C34.
Ta có:2x2+x=3y2+y
⇔ (x-y)+2(x2-y2)=y2
⇔ (x-y)(2x+2y+1)=y2
Gọi ƯCLN(x-y,2x+2y+1) = d
\(\Rightarrow\left\{{}\begin{matrix}x-y⋮d\\2x+2y+1⋮d\end{matrix}\right.\Rightarrow2x+2y+1-2\left(x-y\right)⋮d\)
\(\Rightarrow4y+1⋮d\)
Ta có:(x-y)(2x+2y+1)⋮d2
⇒ y2 ⋮d2 ⇒ y⋮d
Mà 4y+1⋮d
⇒ 1⋮d ⇒x-y,2x+2y+1 là 2 số nguyên tố cùng nhau
⇒x-y,2x+2y+1 là các số chính phương

Bài 2.
Ta có:a2+b2+c2+2abc+1≥2(ab+bc+ca)
⇔ (a2-2ab+b2)+(c2-2c+1)+(2c+2abc-2bc-2ca)≥0
⇔ (a-b)2+(c-1)2+2c(a-1)(b-1)≥0
Vì a,b,c≥0 ⇒ 2c(a-1)(b-1)≥0
Dấu "=" xảy ra ⇔ a=b=c=1
C25: b5: Sử dụng kĩ thuật Côsi ngược dấu:
Ta có: \(\dfrac{1}{2bc^2+1}=1-\dfrac{2bc^2}{2bc^2+1}\ge1-\dfrac{2bc^2}{3\sqrt[3]{b^2c^4}}=1-\dfrac{2\sqrt[3]{bc^2}}{3}\)
Cmtt ta được: \(\dfrac{1}{2ca^2+1}\ge1-\dfrac{2\sqrt[3]{ca^2}}{3};\dfrac{1}{2ab^2+1}\ge1-\dfrac{2\sqrt[3]{ab^2}}{3}\)
\(\Rightarrow VT\ge1-\dfrac{2\sqrt[3]{bc^2}}{3}+1-\dfrac{2\sqrt[3]{ca^2}}{3}+1-\dfrac{2\sqrt[3]{ab^2}}{3}=3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)\)
Ta có: Theo bđt Côsi:
\(\sqrt[3]{bc^2}=\sqrt[3]{b.c.c}\le\dfrac{b+c+c}{3}=\dfrac{b+2c}{3}\)
\(\sqrt[3]{ca^2}=\sqrt[3]{c.a.a}\le\dfrac{c+a+a}{3}=\dfrac{c+2a}{3}\)
\(\sqrt[3]{ab^2}=\sqrt[3]{a.b.b}\le\dfrac{a+b+c}{3}=\dfrac{a+2b}{3}\)
\(\Rightarrow\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}\le\dfrac{b+2c+c+2a+a+2b}{3}=a+b+c=3\)
\(\Rightarrow3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)=1\)
\(\Rightarrow VT\ge1\)
Dấu ''='' xảy ra khi a=b=c=1

Cơ hội kiếm thưởng đây! Với quỹ cộng đồng hoc24 lên tới hơn 450.000đ đến hiện tại, giải thưởng giải Nhất đã đạt ở mức 500.000đ!
Nếu các bạn muốn giúp đỡ cộng đồng qua việc đóng góp giải thưởng, hãy chuyển ngay COIN tới tài khoản này nha :>
Xin cảm ơn các nhà hảo tâm:
- Nguyễn Trần Thành Đạt: 400 COIN.
- Sad Boy: 80 COIN.

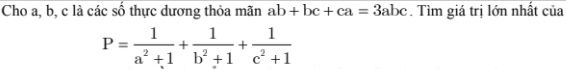
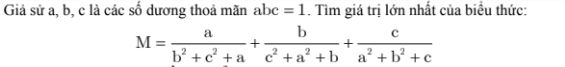




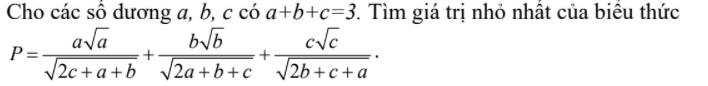

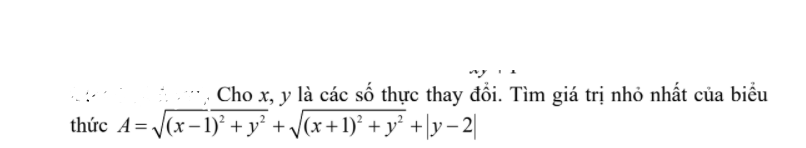
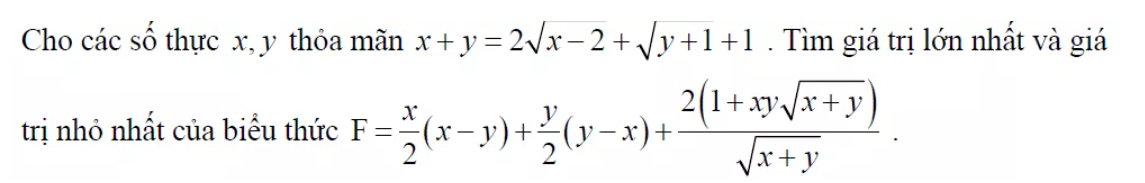
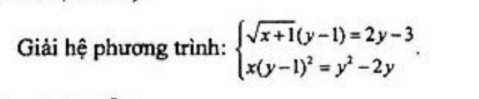
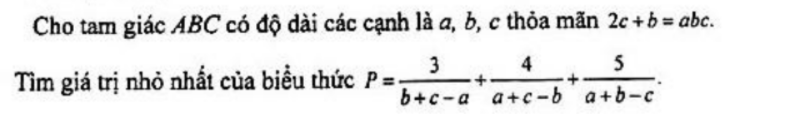
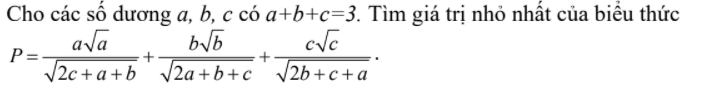

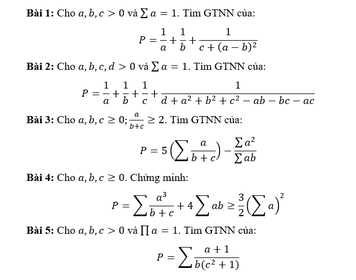



 4)
4) 

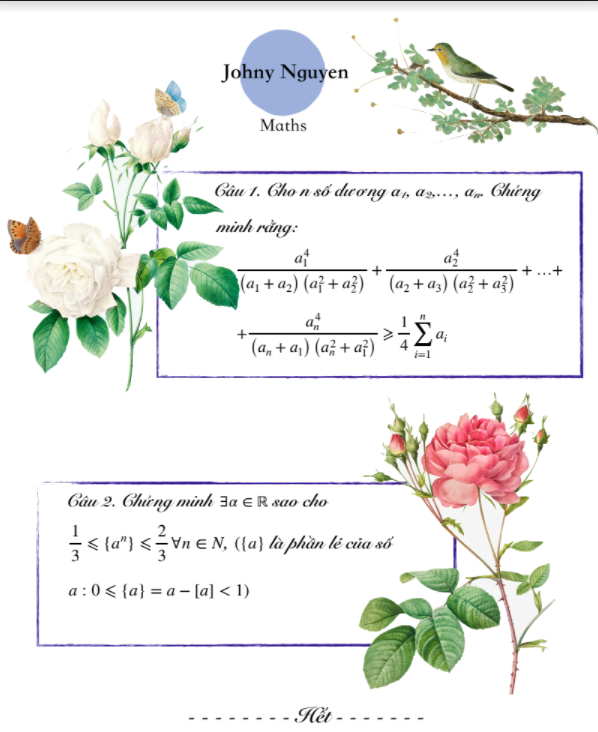





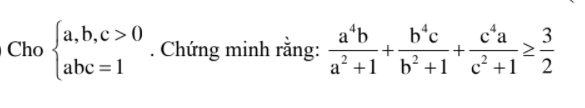
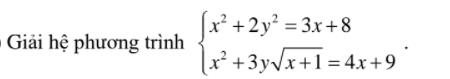
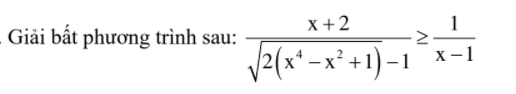

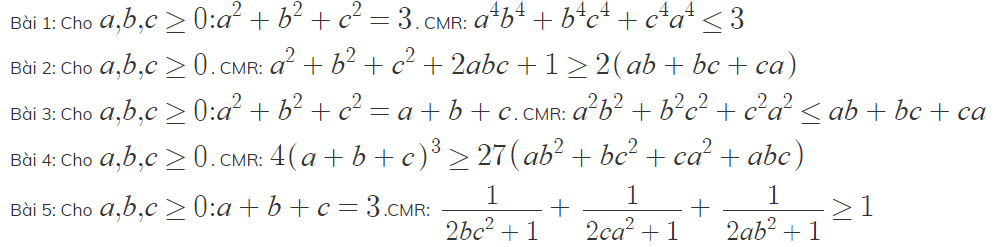

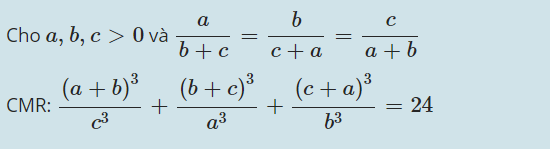
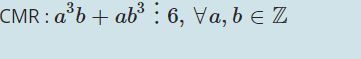
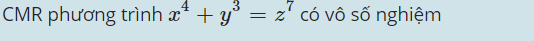
Toán C64, bài 2a)
Toán C64, bài 2b)