Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Nếu tăng cạnh đáy lên 2 lần thì diện tích đáy sẽ tăng lên 4 lần. Gọi diện tích đáy lúc đầu là S ⇒ diện tích đáy sau khi tăng là 4S.
Gọi chiều cao lúc đầu là h ⇒ chiều cao sau khi giảm là h 4 ⇒ Thể tích lúc đầu bằng thể tích lúc sau = S h 3 ⇒ thể tích không thay đổi.

Gọi chiều dài là a, chiều rộng là b ( đơn vị: m)
Có: \(ab=500\)
\(\left(1-20\%\right)a.\left(1+20\%b\right)=\left(1-\frac{1}{5}\right)a.\left(1+\frac{1}{5}\right)b\)
\(=\frac{4}{5}a.\frac{6}{5}b\)
\(=\frac{24}{25}.ab\)
\(=\frac{24}{25}.500=480\)
Do đó diện tích khu vườn giảm đi:
500 - 480 = 20 ( m2)

Tổng đáy lớn và đáy bé là :
360.2 : 12 = 60 ( m )
Tổng số phần bằng nhau là :
2 + 3 = 5 ( phần )
Giá trị một phần là :
60 : 5 = 12 ( m )
Đáy bé là :
12.2 = 24 ( m )
Đáy lớn là :
12.3 = 36 ( m )
Đáp số : Đáy bé : 24 m
Đáy lớn : 36 m

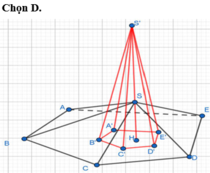
Chọn A.
Phương pháp:
Nhận xét sự thay đổi về thể tích của khối lăng trụ theo cạnh đáy và chiều cao rồi kết luận.
Cách giải:
Gọi cạnh đáy và chiều cao khối lăng trụ đều là a;h thì thể tích V = a 2 h .
Nếu gấp đôi các cạnh đáy đồng thời giảm chiều cao của khối lăng trụ hai lần thì
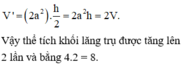

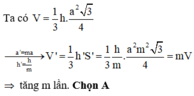


Lời giải:
Nếu tăng độ dài đáy thêm 20% thì độ dài đáy mới bằng $100+20=120$ % độ dài đáy cũ.
Nếu giảm chiều cao 20% thì chiều cao mới bằng $100-20=80$ % chiều cao cũ.
Diện tích mới bằng: $120\times 80:100=96$ % diện tích cũ.
tyyyyyyy