Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi diện tích đáy tháp là S0; diện tích mặt trên của tầng 1; tầng 2; tầng 3; … lần lượt là S1; S2; S3; …; S11.
+ Theo giả thiết diện tích của bề mặt trên mỗi tầng bằng nửa diện tích mặt trên của tầng ngay bên dưới

Vậy diện tích mặt trên của tầng 11 là 6m2.

Chọn C
Diện tích bề mặt của tầng 1 là 12288 2 = 6144 m 2
Diện tích mặt trên cùng là: 6144. 1 2 10 = 6 m 2

Chọn A
Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội q = 1 2 và u 1 = 12 288 2 = 6 144.
Khi đó diện tích mặt trên cùng là : u 11 = u 1 q 10 = 6 144 2 10 = 6

Diện tích mặt đáy tháp là u1 = 12 288 (m2).
Diện tích mặt sàn tầng 2 là: u2 = 12 288.\(\frac{1}{2}\) = 6 144 (m2).
...
Gọi diện tích mặt sàn tầng n là un với n ∈ ℕ*.
Dãy (un) lập thành một cấp số nhân là u1 = 12 288 và công bội \(q = \frac{1}{2}\), có số hạng tổng quát là: un = 12 288.\({\left( {\frac{1}{2}} \right)^{n - 1}}\).
Diện tích mặt tháp trên cùng chính là mặt tháp thứ 11 nên ta có:
u11 = 12 288.\({\left( {\frac{1}{2}} \right)^{11 - 1}}\) = 12 (m2).

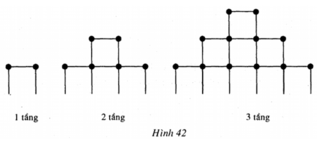
Xây 1 tầng cần 2 que diêm để xếp tầng đế
Xây 2 tầng cần 4 que diêm để xếp tầng đế (4 = 2 + 1.2)
Xây 3 tầng cần 6 que diêm để xếp tầng đế ( 6 = 2 + 2.2)
Xây 100 tầng cần 200 que diêm để xếp tầng đế (200 = 2 + 99.2)

Đáp án A
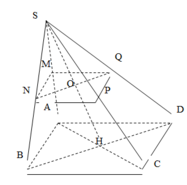
Đặt a> 0 cạnh hình vuông là Dễ thấy
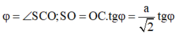
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
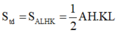
Ta có:


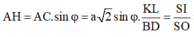
![]()
Theo giả thiết
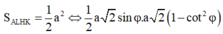
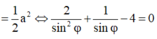
Giải được
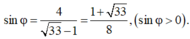
Suy ra φ = a r c sin 33 + 1 8
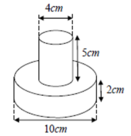

Theo đề bài, diện tích các mặt lập thành một cấp số nhân có số hạng đầu:
u1 = 12288m2 và công bội \(q=\dfrac{1}{2}\).
Vậy diện tích mặt trên cùng là: \(u_{11}=u_1.q^{10}=12288.\left(\dfrac{1}{2}\right)^{10}=12\left(m^2\right)\).