Các câu ở bên trái là các câu khẳng định, có tính đúng sai

Các câu ở bên phải không thể nói là đúng hay sai

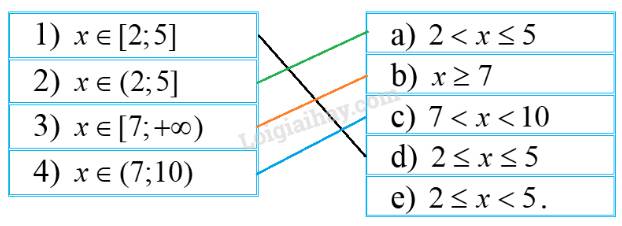
1) \(x \in [2;5] \Leftrightarrow 2 \le x \le 5\). Nối 1) với d)

2) \(x \in (2;5] \Leftrightarrow 2 < x \le 5\). Nối 2) với a)

3) \(x \in [7; + \infty ) \Leftrightarrow x \ge 7\). Nối 3) với b)

4) \(x \in (7;10) \Leftrightarrow 7 < x < 10\). Nối 4) với c)

Tham khảo:

Gọi \(y = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là thành cầu. 

Chọn hệ trục tọa độ Oxy như hình dưới:

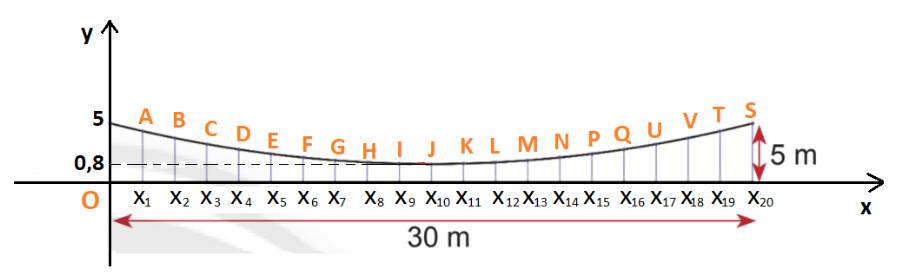
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.

Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.

Khoảng cách giữa hai dây cáp liền kề là: \(30:20 = 1,5\left( m \right)\)

Khi đó: \({x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;\)

Dễ thấy: các điểm có tọa độ (0; 5), (\({x_{10}};0,8\)), \(({x_{20}};5)\) thuộc đồ thị hàm số.

(Trong đó: \({x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.\))

Suy ra:

\(f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5\)

Và \(f(1) = a{.15^2} + b.15 + c = 0,8 \Leftrightarrow 225a + 15b + 5 = 0,8\)

\(f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5\)

Giải hệ phương trình \(\left\{ \begin{array}{l}225a + 15b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.\) ta được \(a = \frac{{7}}{{375}};b =  - \frac{{14}}{{25}}\)

Như vậy \(y = \frac{{7}}{{375}}{x^2} - \frac{{14}}{{25}}x + 5\)

Gọi \({y_0},{y_1},{y_2},..{y_{20}}\) là tung độ của các điểm có hoành độ lần lượt là \({x_0},{x_1},{x_2},..{x_{20}}\)

Ta có:

\(\begin{array}{l}{y_0} = 5\\{y_1} = \frac{{7}}{{375}}.1,{5^2} - \frac{{14}}{{25}}.1,5 + 5\\{y_2} = \frac{{7}}{{375}}.{(2.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {2^2}.\frac{{7}}{{375}}.1,{5^2} - 2.\frac{{14}}{{25}}.1,5 + 5\\...\\{y_n} = \frac{{7}}{{375}}.{(n.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {n^2}.\frac{{7}}{{375}}.1,{5^2} - n.\frac{{14}}{{25}}.1,5 + 5\\ \Rightarrow T = {y_0} + {y_1} + {y_2} + .. + {y_{20}} = 5 + \frac{{7}}{{375}}.1,{5^2}.(1 + {2^2} + ... + {20^2}) - \frac{{14}}{{25}}.1,5.(1 + 2 + ... + 20) + 5.20\end{array}\)

Mà \(1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210\)

\( \Rightarrow T = 5 + \frac{{7}}{{375}}.1,{5^2}.2870 - \frac{{14}}{{25}}.1,5.210 + 5.20 \approx 49,14(m)\)

Do cần tính thêm 5% chiều dài để neo cố định và cần 2 thành mặt cầu nên tổng chiều dài của các dây cáp cần sử dụng là: \(49,14.2.105% = 103,2(m)\)

Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 103,2m.

Với chiều cao dưới 155cm, học sinh nữ chiếm tỉ lệ nhiều hơn (xem hình vẽ 56).

    Với chiều cao trên 160 cm, học sinh nam chiếm tỉ lệ nhiều hơn

Gọi số cần tìm là ab (gạch ngang) , ta có:

ab x 101 = 2ab2

ab x 101 = 2000 + ab x 10 + 2

ab x 101 = 2002 + ab x 10

ab x 101 - ab x 10 = 2002 + ab x 10 - ab x 10

ab x 91 = 2002

Vậy ab = 2002 : 91 = 22

Gọi số phải tìm là ab có :

ab x 101 =2ab2

abab=2ab2

=>a=2 ;b=2

=>ab=22

=>Số phải tìm là 22

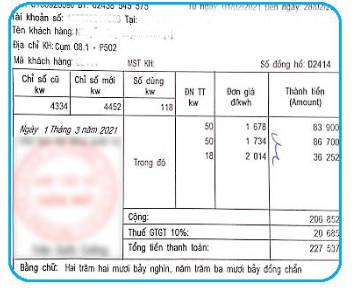
Quan sát hóa đơn ta thấy:

Tổng lượng điện tiêu thụ trong tháng là: 50 + 50 + 18 = 118 (kW).

Số tiền phải trả (chưa tính thuế giá trị gia tăng) là 206 852 đồng.

Giá tiền điện được tính theo bậc thang cho từng số lượng điện đã dùng, cụ thể:

Dùng 50 kW đầu thì đơn giá là 1 678 đồng/ 1 kW.

Dùng 50 kW tiếp theo thì đơn giá là 1 734 đồng/ 1 kW.

Dùng 100 kW tiếp thì đơn giá là 2 014 đồng/ 1 kW.

…

Ở hóa đơn điện trên kia, người sử dụng điện dùng 118 kW, có nghĩa phải trả theo 3 bậc.

Nên ta tính số tiền điện bằng cách thực hiện phép tính:

50 . 1 678 + 50 . 1 734 + 18 . 2 014 = 206 852 (đồng)

Vậy ta mô tả được sự phụ thuộc của số tiền điện phải trả vào tổng lượng điện tiêu thụ như trên.

Các câu ở bên trái là các câu khẳng định, có tính đúng sai

Các câu ở bên phải không thể nói là đúng hay sai.

Không có hình vẽ bạn?

Hình P Đi xuống á