
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}}-\sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(3\sqrt{3}-4\right)\left(2\sqrt{3}-1\right)}{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}}\)\(-\sqrt{\dfrac{\left(\sqrt{3}+4\right)\left(5+2\sqrt{3}\right)}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}}\)
\(=\sqrt{\dfrac{18-3\sqrt{3}-8\sqrt{3}+4}{\left(2\sqrt{3}\right)^2-1}}\)\(-\sqrt{\dfrac{5\sqrt{3}+6+20+8\sqrt{3}}{5^2-\left(2\sqrt{3}\right)^2}}\)
\(=\sqrt{\dfrac{22-11\sqrt{3}}{11}}\)\(-\sqrt{\dfrac{26+13\sqrt{3}}{13}}\)
\(=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}-\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}+1}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)

2:
BC^2*MB
\(=\dfrac{BH^2}{BA}\cdot BC^2=\left(\dfrac{BA^2}{BC}\right)^2\cdot\dfrac{BC^2}{BA}\)
\(=\dfrac{BA^4}{BA}\cdot\dfrac{BC^2}{BC^2}=BA^3\)
=>\(MB=\dfrac{BA^3}{BC^2}\)

Lời giải:
Cộng 3 PT lại ta có:
$x(a+b+c)+y(a+b+c)=a+b+c$
$\Leftrightarrow (a+b+c)(x+y-1)=0$
$\Rightarrow a+b+c=0$ hoặc $x+y-1=0$
TH1: $a+b+c=0\Leftrightarrow a+b=-c$
Khi đó: $a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=3abc$
$\Rightarrow \frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=3$ (đpcm)
TH2: $x+y-1=0\Leftrightarrow y=1-x$
Thay vô hpt \(\left\{\begin{matrix} ax+b(1-x)=c\\ bx+c(1-x)=a\\ cx+a(1-x)=b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x(a-b)=c-b\\ x(b-c)=a-c\\ x(c-a)=b-a\end{matrix}\right.\)
\(\Rightarrow x^3(a-b)(b-c)(c-a)=(c-b)(a-c)(b-a)=-(a-b)(b-c)(c-a)\)
\(\Leftrightarrow (a-b)(b-c)(c-a)(x^3+1)=0\)
Nếu $a-b=0$ thì kéo theo $b-c=c-a=0$
$\Rightarrow a=b=c$
Nếu $b-c=0; c-a=0$ thì tương tự
Nếu $x^3+1=0\Leftrightarrow x=-1$
$\Rightarrow b-a=c-b=a-c\Rightarrow a=b=c$
Tóm lại $a=b=c$
Do đó: $\frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=1+1+1=3$ (đpcm)

\(P=\left(x^2+2x\right)\left(y^2-4y\right)+5\left(x^2+2x\right)+4\left(y^2-4y\right)+2021\)
\(=\left[\left(x+1\right)^2-1\right]\left[\left(y-2\right)^2-4\right]+5\left(x+1\right)^2+4\left(y-2\right)^2+2000\)
\(=\left(x+1\right)^2\left(y-2\right)^2+\left(x+1\right)^2+3\left(y-2\right)^2+2024\ge2024\)
\(P_{min}=2024\) khi \(\left(x;y\right)=\left(-1;2\right)\)


Xét ΔABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{AB^2+\left(2AB\right)^2}=AB\sqrt{5}\)
Mà:
\(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}=\dfrac{AB}{AB\sqrt{5}}=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\\cosC=\dfrac{AC}{BC}=\dfrac{2AB}{AB\sqrt{5}}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\\tanC=\dfrac{AB}{AC}=\dfrac{AB}{2AB}=\dfrac{1}{2}\\cotC=\dfrac{AC}{AB}=\dfrac{2AB}{AB}=2\end{matrix}\right.\)
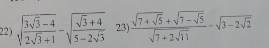
 Nhờ mn giúp mình câu 1c và câu 2 ạ. Thanks
Nhờ mn giúp mình câu 1c và câu 2 ạ. Thanks

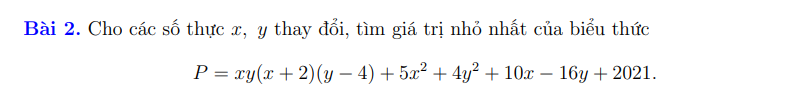


Ta có: \(x+y+z=1\)mà \(x,y,z\)không âm nên \(0\le x,y,z\le1\)
suy ra \(x^2\le x,y^2\le y,z^2\le z\)
\(S=\sqrt{3x^2 +1}+\sqrt{3y^2+1}+\sqrt{3z^2+1}\)
\(\le\sqrt{x^2+2x+1}+\sqrt{y^2+2y+1}+\sqrt{z^2+2z+1}\)
\(=\left|x+1\right|+\left|y+1\right|+\left|z+1\right|\)
\(=x+y+z+3=4\)
Dấu \(=\)xảy ra khi \(\hept{\begin{cases}x=1\\y=z=0\end{cases}}\)và các hoán vị.