
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chu vi của tam giác abc là
ab+bc+c=25 (1)
chu vi của tam giác acd là (2)
ac+cd+da=17 (3)
chu vi của tứ giác abcd là
ab+bc+cd+da=32
từ (1) và (2) ta có :
ab+bc+ac+ac+cd+da=25+27=52
=>(ab=bc=cd=da)+2ac=52 (4)
từ (1) và (4)
<=> 32+2ac=52
=>2ac =52 - 32 =20
=>ac=20:2=10
vậy ac = 10cm

TL:
Vì nó cầm dao và đấm vào ngực nó (đười ươi hay làm thế).
HT~
@@@@@@
Vì nó cầm dao và đấm đấm vào ngực của nó.
Thói quen mà. gần giống king kong ớ bạn
HT

thực ra đề gốc hỏi x+y có phải là số chính phương hay không, x,y,z thuộc N*, có bạn làm thế này:
\(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\Leftrightarrow z.\left(x+y\right)=xy\)
Giả sử x+y là số chính phương. Đặt x+y=k2
mà \(z.\left(x+y\right)=xy\)
\(\Leftrightarrow zk^2=xy\)
Vì x,y là số nguyên tố => 1 trong 2 số chia hết cho k2 vì x,y,z thuộc N*
Giả sử x=n.k2 (n thuộc N*)
mà \(zk^2=xy\)
\(\Leftrightarrow zk^2=n.k^2.y\Leftrightarrow z=n.y\Leftrightarrow\frac{z}{y}=n\), vì x,y là 2 số nguyên tố cùng nhau => n không thuộc N*(vô lí)
vậy x+y ko phải số chính phương
Bạn đó làm đã đúng chưa, nếu sai hãy sửa lại :v
Thử, đúng hay sai thì tùy, mình mới học sơ sơ dạng này thôi, nếu sai xin đừng bốc phốt...:v
Theo đề bài\(z\left(x+y\right)=xy\Leftrightarrow x+y=\frac{xy}{z}\) và (x;y;z) = 1
Giả sử x + y là số chính phương khi đó \(\frac{xy}{z}=k^2\left(k\inℕ^∗\right)\Leftrightarrow xy=k^2.z\)
Suy ra xy chia hết cho z. Mà x, y, z nguyên tố cùng nhau nên x và y đều không chia hết cho z.
\(\Rightarrow xy=z\). Khi đó \(\left(x;y;z\right)=1\Leftrightarrow\left(x;y\right)=\left(y;z\right)=1\Leftrightarrow\left(x;y\right)=\left(y;xy\right)=1\) (vô lí vì
\(\left(y;xy\right)=y\))
Vậy ko tồn tại x, y,z..

Trả lời : a.Có lợi vì nói dễ bị ngã chứ chưa ngã có nghĩa là lực ma sát nghỉ sinh ra ở đây giúp ta đứng vững và khi di chuyển sẽ ko bị ngã.
Trả lời : b.Giày đi mãi đế bị mòn vì ma sát của mặt đường với đế giày làm mòn đế. Ma sát trong trường hợp này là có hại.
mong bạn
a.Có lợi vì nói dễ bị ngã chứ chưa ngã có nghĩa là lực ma sát nghỉ sinh ra ở đây giúp ta đứng vững và khi di chuyển sẽ ko bị ngã.
b.Giày đi mãi đế bị mòn vì ma sát của mặt đường với đế giày làm mòn đế.Ma sát trong trường hợp này có hại.

1:
a: =x^2+3x+4x+12
=x(x+3)+4(x+3)
=(x+3)(x+4)
b: =4x^2-4x-5x+5
=4x(x-1)-5(x-1)
=(x-1)(4x-5)
c: =2x^2-3x-4x+6
=x(2x-3)-2(2x-3)
=(2x-3)(x-2)
3:
a: =2x^2-6xy+xy-3y^2
=2x(x-3y)+y(x-3y)
=(x-3y)(2x+y)
b: =x^2+3xy-xy-3y^2
=x(x+3y)-y(x+3y)
=(x+3y)*(x-y)
c: =6x^2+4xy-3xy-2y^2
=2x(3x+2y)-y(3x+2y)
=(3x+2y)(2x-y)

mk nghĩ là người đàn ông vì đàn bà thì hóa trang thành trai đâu có j lạ
nhưng người đàn ông mặc váy, đeo giày cao gót sẽ ko quen

\(P=a\left(2a-3\right)-2a\left(a+1\right)+5\)
\(=2a^2-3a-2a^2-2a+5\)
\(=\left(2a^2-2a^2\right)-\left(3a+2a\right)+5\)
\(=-5a+5=-5\left(a-1\right)⋮5\)

Xét △ACD và △BDC có:
\(\begin{matrix}AD=BC\left(gt\right)\\\hat{D}=\hat{C}\left(gt\right)\\CD\text{ }chung\end{matrix}\Rightarrow\Delta ACD=\Delta BDC\left(c.c.c\right)\Rightarrow\hat{ACD}=\hat{BDC}\text{ }hay\text{ }\text{ }\hat{ICD}=\hat{IDC}\)
⇒ △ICD cân tại I ⇒ \(ID=IC\left(1\right)\)
△KCD có: \(\hat{C}=\hat{D}\) ⇒ △KCD cân tại K ⇒ \(KD=KC\left(2\right)\)
Từ (1) và (2). Suy ra KI là đường trung trực của CD (3)
Tương tự ta cũng có: \(IA=IB;KA=KB\). Suy ra KI là đường trung trực của AB (4)
Từ (3) và (4). Vậy: KI là đường trung trực của AB và CD
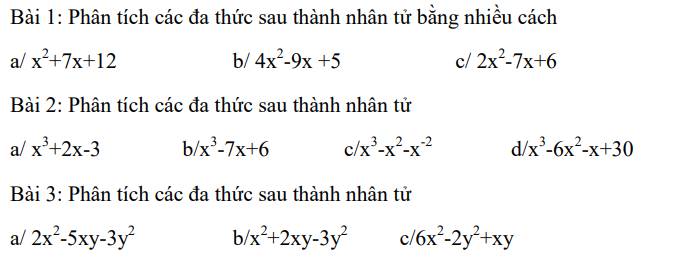
không
vì chưa có ghi lại cảnh ông già vào từng nhà trong khi FBI và CIA có thể theo dõi
Ông già Noel hoàn toàn có thật.