Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phân tích đa thức thành nhân tử:
a) (x-1)(x-2)(x-3)(x-4)+1
b) (x2+3x+2)(x2+7x+12)+1
c) 12x2-3xy-8xz+2yz

a) \(A=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)+1\)
\(A=\left[\left(x-1\right)\left(x-4\right)\right]\left[\left(x-2\right)\left(x-3\right)\right]+1\)
\(A=\left(x^2-5x+4\right)\left(x^2-5x+6\right)+1\)
Đặt \(a=x^2-5x+5\)
\(\Leftrightarrow A=\left(a-1\right)\left(a+1\right)+1\)
\(\Leftrightarrow A=a^2-1^2+1\)
\(\Leftrightarrow A=a^2\)
Thay \(a=x^2-5x+5\)vào A ta có :
\(A=\left(x^2-5x+5\right)^2\)
b) \(B=\left(x^2+3x+2\right)\left(x^2+7x+12\right)+1\)
\(B=\left(x^2+x+2x+2\right)\left(x^2+3x+4x+12\right)+1\)
\(B=\left[x\left(x+1\right)+2\left(x+1\right)\right]\left[x\left(x+3\right)+4\left(x+3\right)\right]+1\)
\(B=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
Làm tương tự câu a)
c) \(12x^2-3xy-8xz+2yz\)
\(=3x\left(4x-y\right)-2z\left(4x-y\right)\)
\(=\left(4x-y\right)\left(3x-2z\right)\)

a) Áp dụng HĐT 1 thu được ( 2 x + y ) 2 .
b) Áp dụng HĐT 3 với A = 2x + l; B = x - l thu được
[(2x +1) + (x -1)] [(2x +1) - (x -1)] rút gọn thành 3x(x + 2).
c) Ta có: 9 - 6x + x 2 - y 2 = ( 3 - x ) 2 - y 2 = (3 - x - y)(3 -x + y).
d) Ta có: -(x + 2) + 3( x 2 - 4) = -{x + 2) + 3(x + 2)(x - 2)
= (x + 2) [-1 + 3(x - 2)] = (x + 2)(3x - 7).

\(1,\\ 12x^6y^3:4x^3y=3x^3y^2\\ \left(x+1\right)\left(x^2-x+1\right)=x^3+1\\ 2x^2y\left(x^2+3xy\right)=3x^4y+6x^3y^2\\ 2,\\ a,=2xy\left(2x+3y-4\right)\\ b,=\left(x-3\right)\left(x+y\right)\\ c,=\left(x-2\right)\left(x+2\right)+y\left(x-2\right)=\left(x+y+2\right)\left(x-2\right)\\ d,=x^2-2x-5x+10=\left(x-2\right)\left(x-5\right)\\ 3,\\ a,\Leftrightarrow x^2-x^2+2x=2\\ \Leftrightarrow2x=2\Leftrightarrow x=1\\ b,\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a: \(=5x\left(xy^2+3x+6y^2\right)\)
b: \(=\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(x+3-x-2\right)=\left(x-2\right)\)
c: \(=\left(x-3\right)\left(x-4\right)\)
d: \(=x\left(x^2-2xy+y^2-9\right)\)
=x(x-y-3)(x-y+3)
e: \(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)
f: \(=\left(x-4\right)\left(x+3\right)\)

-Đặt \(t=\left(x^2-x+1\right)\)
\(\left(x^2-x+1\right)^2-5x\left(x^2-x+1\right)+4x^2\)
\(=t^2-5xt+4x^2\)
\(=t^2-4xt-xt+4x^2\)
\(=t\left(t-4x\right)-x\left(t-4x\right)\)
\(=\left(t-4x\right)\left(t-x\right)\)
\(=\left(x^2-x+1-4x\right)\left(x^2-x+1-x\right)\)
\(=\left(x^2-5x+1\right)\left(x^2-2x +1\right)\)
\(=\left(x^2-5x+1\right)\left(x-1\right)^2\)
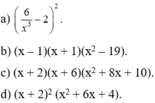
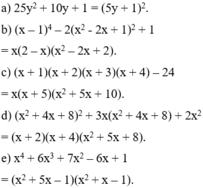
\(\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)-80=\left(x^2-5x+4\right)\left(x^2-5x+6\right)-80\)
Đặt \(x^2-5x+4=t\), ta có:
\(t\left(t+2\right)-80=t^2-2t+1-81=\left(t-1\right)^2-9^2=\left(t-1-9\right)\left(t-1+9\right)=\left(t-10\right)\left(t+8\right)\)
\(=\left(x^2-5x+4-10\right)\left(x^2-5x+4+8\right)=\left(x^2-5x-6\right)\left(x^2-5x+12\right)\)
\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt x2 + x + 1 = t, ta có:
t(t + 1) - 12
= t2 + t + 1/4 - 49/4
= (t + 1/2)2 - (7/2)2
= (t + 1/2 + 7/2)(t + 1/2 - 7/2)
= (t + 4)(t - 3)
nhân váo như bình thường sau đó bấm máy tính shift solve =? rồi chia hoocne