Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có ln ( x + 1 ) = 2 ⇔ x + 1 = e 2
⇔ x = e 2 - 1
Chọn đáp án B.

Đáp án D.
Cách 1: Tư duy tự luận
Điều kiện: x 2 > 0 ⇔ x ≠ 0.
Bất phương trình
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ 2 x 2 − 4 − 1 < 0 ln ( x 2 ) > 0 2 x 2 − 4 − 1 > 0 ln ( x 2 ) < 0 ⇔ x 2 − 4 < 0 x 2 > 1 x 2 − 4 > 0 x 2 < 1 ( L )
⇔ ( x − 2 ) ( x + 2 ) < 0 ( x − 1 ) ( x + 1 ) > 0 ⇔ − 2 < x < 2 x > 1 x < − 1 ⇔ 1 < x < 2 − 2 < x < − 1
Vậy tập nghiệm của bất phương trình là S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
Cách 2: Sử dụng máy tính cầm tay
Nhập vào màn hình biểu thức 2 x 2 − 4 − 1 . ln ( X 2 ) và CALC với X = − 2 ; − 1 ; 1 ; 2.

Ta xét dấu của biểu thức 2 X 2 − 4 − 1 . ln ( X 2 ) trên mỗi khoảng ( − ∞ ; − 2 ) , ( − 2 ; − 1 ) , ( − 1 ; 1 ) , ( 1,2 ) , ( 2 ; + ∞ ) .
Tiếp tục dùng CACL:

Vậy
( 2 x 2 − 4 − 1 ) . ln ( x 2 ) < 0 ⇔ x ∈ ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .

Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


Đáp án A.
Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x0 là: ![]()
Cách giải: Ta có: 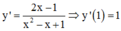
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 là: ![]()

Bất phương trình m > f(x) - ln(-x) đúng với mọi x ∈ - 1 ; - 1 e
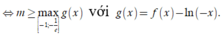
Ta có ![]()
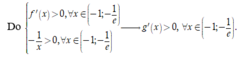
Suy ra hàm số g(x) đồng biến trên ![]()
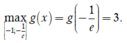
Chọn D.
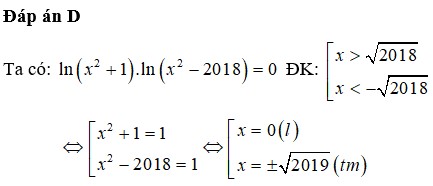

Đáp án A