
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{3}{x-1}=\dfrac{3\cdot9}{9\cdot\left(x-1\right)}=\dfrac{27}{9\left(x-1\right)}\)
\(\dfrac{4}{3x-3}=\dfrac{12}{9x-9}=\dfrac{12}{9\left(x-1\right)}\)
\(\dfrac{10}{9-9x}=\dfrac{-10}{9x-9}=-\dfrac{10}{9\left(x-1\right)}\)
b: \(\dfrac{3}{2\left(x-3\right)}=\dfrac{3x-9}{2\left(x-3\right)^2}\)
\(\dfrac{3x-2}{x^2-6x+9}=\dfrac{6x-4}{2\left(x-3\right)^2}\)
c: \(\dfrac{3}{x^2+2x+1}=\dfrac{3}{\left(x+1\right)^2}=\dfrac{3x}{x\left(x+1\right)^2}\)
\(-\dfrac{2}{x^2+x}=\dfrac{-2}{x\left(x+1\right)}=\dfrac{-2\left(x+1\right)}{x\left(x+1\right)^2}\)

a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)

Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)

\(a.\) Ta có:
\(MTC:\) \(\left(x+1\right)\left(x+2\right)\)
Do đó
\(\frac{3x}{x+1}=\frac{3x\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\frac{x+4}{x+2}=\frac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x+2\right)}\)
\(b.\) Ta có:
\(x^2+x=x\left(x+1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
nên \(MTC:\) \(x\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\frac{5}{x^2+x}=\frac{5}{x\left(x+1\right)}=\frac{5\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(\frac{6}{x^2-1}=\frac{6}{\left(x-1\right)\left(x+1\right)}=\frac{6x}{x\left(x-1\right)\left(x+1\right)}\)
\(c.\) Ta có:
\(x^2-5x+4=x^2-x-4x+4=x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(x-4\right)\)
\(2x^2-8x=2x\left(x-4\right)\)
nên \(MTC:\) \(2x\left(x-1\right)\left(x-4\right)\)
Do đó:
\(\frac{4}{x^2-5x+4}=\frac{4}{\left(x-1\right)\left(x-4\right)}=\frac{8x}{2x\left(x-1\right)\left(x-4\right)}\)
\(\frac{x+1}{2x^2-8x}=\frac{x+1}{2x\left(x-4\right)}=\frac{\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)\left(x-4\right)}\)
Làm nốt d :P
\(\frac{x+3}{2x^2-15x-8};\frac{3}{x^2-8x}\)
Ta có : \(2x^2-15x-8=\left(2x+1\right)\left(x-8\right)\)
\(x^2-8x=x\left(x-8\right)\)
MTC : \(x\left(x-8\right)\left(2x+1\right)\)
\(\frac{x+3}{2x^2-15x-8}=\frac{x+3}{\left(2x+1\right)\left(x-8\right)}=\frac{x^2+3x}{x\left(x-8\right)\left(2x+1\right)}\)
\(\frac{3}{x^2-8x}=\frac{3}{x\left(x-8\right)}=\frac{6x+3}{x\left(x-8\right)\left(2x+1\right)}\)

a) MTC: \(12x^3y^3\)
\(\dfrac{3}{4x^3y^2}=\dfrac{3\cdot3y}{4x^3y^2\cdot3y}=\dfrac{9y}{12x^3y^3}\)
\(\dfrac{2}{3xy^3}=\dfrac{2\cdot4x^2}{3xy^3\cdot4x^2}=\dfrac{8x^2}{12x^3y^3}\)
b) MTC: \(x\left(x-3\right)^2\)
\(\dfrac{5}{x^2-6x+9}=\dfrac{5}{\left(x-3\right)^2}=\dfrac{5x}{x\left(x-3\right)^2}\)
\(\dfrac{3}{x^2-3x}=\dfrac{3}{x\left(x-3\right)}=\dfrac{3\left(x-3\right)}{x\left(x-3\right)^2}=\dfrac{3x-9}{x\left(x-3\right)^2}\)

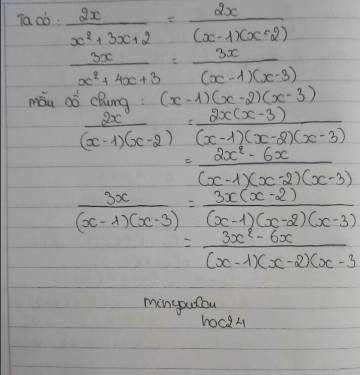

a: ĐKXĐ: \(x\notin\left\{4;-4\right\}\)
\(\dfrac{7}{4x+16}=\dfrac{7}{4\left(x+4\right)}=\dfrac{7\left(x-4\right)}{4\left(x+4\right)\left(x-4\right)}\)
\(\dfrac{11}{x^2-16}=\dfrac{11\cdot4}{4\left(x^2-16\right)}=\dfrac{44}{4\left(x-4\right)\left(x+4\right)}\)
b: \(\dfrac{6}{x\left(x+3\right)^2};\dfrac{x-3}{2x\left(x+3\right)^2}\)
ĐKXĐ: \(x\notin\left\{0;-3\right\}\)
\(\dfrac{6}{x\left(x+3\right)^2}=\dfrac{6\cdot2}{2x\left(x+3\right)^2}=\dfrac{12}{2x\left(x+3\right)^2}\)
\(\dfrac{x-3}{2x\left(x+3\right)^2}=\dfrac{x-3}{2x\left(x+3\right)^2}\)
c: \(\dfrac{-6}{1-x};\dfrac{3x}{x^2+x+1};\dfrac{x^2-3x+5}{x^3-1}\)
ĐKXĐ: \(x\ne1\)
\(-\dfrac{6}{1-x}=\dfrac{6}{x-1}=\dfrac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{6x^2+6x+6}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{3x}{x^2+x+1}=\dfrac{3x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{3x^2-3x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{x^2-3x+5}{x^3-1}=\dfrac{x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
d: \(\dfrac{17}{5x};\dfrac{24}{x-2y};\dfrac{x-y}{8y^2-2x^2}\)
ĐKXĐ: \(x\ne0;x\ne\pm2y\)
\(\dfrac{17}{5x}=\dfrac{17\cdot2\left(x-2y\right)\left(x+2y\right)}{5x\cdot2\cdot\left(x-2y\right)\left(x+2y\right)}=\dfrac{34\left(x^2-4y^2\right)}{10x\left(x-2y\right)\left(x+2y\right)}\)
\(\dfrac{24}{x-2y}=\dfrac{24\cdot10x\left(x+2y\right)}{10x\left(x-2y\right)\left(x+2y\right)}=\dfrac{240x\left(x+2y\right)}{10x\left(x-2y\right)\left(x+2y\right)}\)
\(\dfrac{x-y}{8y^2-2x^2}=\dfrac{-\left(x-y\right)}{2x^2-8y^2}=\dfrac{-\left(x-y\right)}{2\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{-5x\left(x-y\right)}{10x\left(x-2y\right)\left(x+2y\right)}=\dfrac{-5x^2+5xy}{10x\left(x-2y\right)\left(x+2y\right)}\)