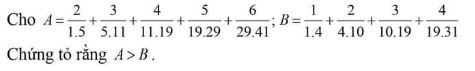Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{2^3.3}{2^2.3^2.5}=\frac{2}{3.5}=\frac{2}{15}\)
Thiếu dấu nhân ở chỗ \(2^2.3^2\)nha

\(\frac{1212}{3131}=\frac{1212:101}{3131:101}=\frac{12}{31}\)

\(\frac{3^{10}.\left(-5\right)^{21}}{\left(-5\right)^{20}.3^{12}}=\frac{3^{10}.\left(-5\right)^{20}.\left(-5\right)}{\left(-5\right)^{20}.3^{10}.3^2}=\frac{-5}{3^2}=-\frac{5}{9}\)

1/2 . P = 1/2.6 + 1/6.10 + 1/10.14 + ... + 1/198.202
4.1/2. P= 4/2.6 + 4/6.10 + 4/10.14 + ... + 4/198.202
2P=1/2-1/6+1/6-1/10+1/10-1/14+...+1/198-1/202
2P=1/2-1/202=50/101
P=50/101:2=50/101.1/2=25/101

\(\frac{-5^3\cdot40\cdot4^3}{135\cdot\left(-2\right)^{14}\left(-100\right)^0}=\frac{-125\cdot2^3\cdot5\cdot\left(2^2\right)^3}{5\cdot27\cdot2^{14}\cdot1}=\frac{-125\cdot2^6}{27\cdot2^{11}}=\frac{-125}{27\cdot2^5}=\frac{-125}{864}\)
\(\frac{\left(-5\right)^3.40.4^3}{135.\left(-2\right)^{14}.\left(-100\right)^0}\)\(=\frac{\left(-5\right)^3.5.2^3.2^6}{3^3.5.2^{14}.1}\)\(=\frac{-125}{864}\)

a) e chỉ cần nhân chúng lại với nhau = cách tách từng cái ra
b)đặt 4/2.5+4/5.8+4/8.11+......+4/62.65 là S
\(.S=\frac{4}{3}\left(\frac{3}{2.5}+\frac{3}{5.8}+...+\frac{3}{62.65}\right)\)
\(S=\frac{4}{3}\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{62}-\frac{1}{65}\right)\)
\(S=\frac{4}{3}\left(\frac{1}{2}-\frac{1}{65}\right)\)
\(S=\frac{4}{3}\left(\frac{65}{130}-\frac{2}{130}\right)\)
\(S=\frac{4}{3}\left(\frac{63}{130}\right)\)
\(S=\frac{42}{65}\)
Bài 2 : \(\frac{15+a}{29+a}=\frac{3}{5}\)\(\Leftrightarrow\left(15+a\right)5=\left(29+a\right)3\Leftrightarrow75+5a=87+3a\Leftrightarrow5a-3a=87-75\Rightarrow2a=12\Rightarrow a=6\)
vậy a =6

\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)

\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
Ta có: \(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(2A=1-\dfrac{1}{5}+\dfrac{1}{5}+...+\dfrac{1}{29}-\dfrac{1}{41}\)
\(2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(A=\dfrac{20}{41}\)
Lại có: \(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(3B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+...+\dfrac{1}{19}-\dfrac{1}{31}\)
\(3B=1-\dfrac{1}{31}=\dfrac{30}{31}\)
\(B=\dfrac{10}{31}\)
Vì \(\dfrac{20}{41}>\dfrac{10}{31}\) nên...

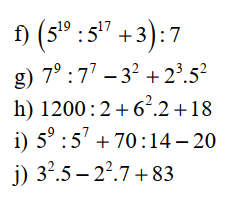 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim