Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Ta có: \(\frac{1313}{1515}< \frac{1313}{1428}< \frac{1326}{1428}\Rightarrow\frac{1313}{1515}< \frac{1326}{1428}\)
b)Ta có: \(1-\frac{119}{120}=\frac{1}{120}< 1-\frac{118}{119}=\frac{1}{119}\Rightarrow\frac{119}{120}>\frac{118}{119}\)
c)Ta có: \(\frac{222}{555}< \frac{222}{444}< \frac{333}{444}\Rightarrow\frac{222}{555}< \frac{333}{444}\)

a)\(\frac{1313}{1515}=\frac{13\times101}{15\times101}=\frac{13}{15}\)
\(\frac{1326}{1428}=\frac{1326:102}{1428:102}=\frac{13}{14}\)
DO \(\frac{13}{14}>\frac{13.}{15}\) nên \(\frac{1326}{1428}>\frac{1313}{1515}\)
\(b\))\(\frac{222}{555}\) và \(\frac{333}{444}\)
\(\frac{222}{555}=\frac{2\times111}{5\times111}=\frac{2}{5}\)
\(\frac{333}{444}=\frac{3\times111}{4\times111}=\frac{3}{4}\)
DO \(\frac{2}{5}< \frac{3}{4}\) nên \(\frac{222}{555}< \frac{333}{444}\)

\(\dfrac{3}{7},\dfrac{2}{3},\dfrac{12}{12},\dfrac{7}{6}\)
các số từ bé đấn lớn là
\(\dfrac{3}{7};\dfrac{2}{3};\dfrac{12}{12};\dfrac{7}{6}\)

a. \(\dfrac{18}{25};\dfrac{25}{25};\dfrac{49}{25}\)
Mình làm trước câu a
a)\(\dfrac{18}{25}< \dfrac{25}{25}< \dfrac{49}{25}\)
b)\(\dfrac{89}{90}< \dfrac{110}{110}< \dfrac{4}{3}\)
c)\(\dfrac{1}{100}< \dfrac{3}{100}< \dfrac{46}{100}< \dfrac{49}{100}< \dfrac{103}{100}< \dfrac{110}{100}\)

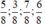


\(\dfrac{555}{1110};\dfrac{333}{444};\dfrac{444}{555};\dfrac{118}{119};\dfrac{119}{120}\)
\(\dfrac{444}{555}\) = \(\dfrac{444:111}{555:111}\) = \(\dfrac{4}{5}\) = 1 - \(\dfrac{1}{5}\)
\(\dfrac{333}{444}\) = \(\dfrac{333:111}{444:111}\) = \(\dfrac{3}{4}\) = 1 - \(\dfrac{1}{4}\)
\(\dfrac{118}{119}\) = 1 - \(\dfrac{1}{119}\)
\(\dfrac{119}{120}\) = 1 - \(\dfrac{1}{120}\)
\(\dfrac{555}{1110}\) = \(\dfrac{555:555}{1110:555}\) = \(\dfrac{1}{2}\) = 1 - \(\dfrac{1}{2}\)
Vì : \(\dfrac{1}{2}>\dfrac{1}{3}>\dfrac{1}{4}>\) \(\dfrac{1}{119}\) > \(\dfrac{1}{120}\)
nên \(\dfrac{555}{1110}>\dfrac{333}{444}>\)\(\dfrac{444}{555}\) > \(\dfrac{118}{119}\) > \(\dfrac{119}{120}\)
Vậy Các phân số đã cho được sắp xếp theo thứ tự từ bé đến lớn là:
\(\dfrac{555}{1110}\); \(\dfrac{333}{444}\); \(\dfrac{444}{555}\); \(\dfrac{118}{119}\); \(\dfrac{119}{120}\)