
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.

Xếp 6 học sinh trường A vào 1 dãy ghế: 6! cách
Xếp 6 học sinh trường B vào dãy còn lại: 6! cách
Lúc này hai học sinh đối diện luôn khác trường, có 6 cặp như vậy, mỗi cặp có 2 cách hoán vị nên có \(2^6\) cách hoán vị
Tổng cộng: \(6!.6!.2^6\) cách xếp thỏa mãn

Số cách sắp xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế là số hoán vị của 4 phần tử \(P4=4!=24\left(cách\right)\)

Đáp án là A
Xếp bạn Chi ngồi giữa có 1 cách.
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là
một hoán vị của 4 phần tử nên có có 4! = 24 cách.
Vậy có 1.24 = 24 cách xếp.

Chọn A
Lời giải. Xếp bạn Chi ngồi giữa có 1 cách.
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! cách.
Vậy có 24 cách xếp

Chọn A
Giả sử khi xếp 10 người vào một bàn tròn, hai cách sắp xếp được xem là như nhau nếu cách này nhận được từ cách kia bằng cách xoay bàn đi một góc nào đó.
Bài toán trên được chia thành các công đoạn sau:
Công đoạn 1: Chọn 10 người trong 20 người đã cho để xếp vào bàn tròn A: có C 20 10 cách.
Công đoạn 2: Sắp xếp 10 người vừa chọn được ở công đoạn 1 vào bàn tròn A: có 9! cách.
Công đoạn 3: Sắp xếp 10 người còn lại vào bàn tròn B: có 9! cách.
Vậy số cách sắp xếp là: C 20 10 .9!.9! cách.


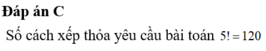
Đáp án C.