Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào bảng tần số, ta thấy tần số lớn nhất là 47 ứng với cỡ áo 39. Vậy mốt của mẫu số liệu là 39.

Dễ thấy: Hoa hồng nhung là loại hoa bán được nhiều nhất trong dịp năm nay, do đó cửa hàng nên nhập loại hoa này nhiều nhất để bán vào dịp 14 tháng 2 năm sau.

Ta sắp xếp dãy số áo bán được theo dãy tăng dần:
36, 36, 36, …, 36, 37, 37, …, 37, 38, 38, …, 38, …., 42, 42.
Dãy số gồm 465 số nên số trung vị là số đứng ở vị trí thứ 233.
Số thứ 233 là số 39.
Vậy Me = 39.

Cỡ áo mà cửa hàng bác Tâm bán được nhiều nhất trong tháng đầu tiên là cỡ áo: 40 (số áo bán được là 81).

a)
Bảng tần số:
Cỡ giày | 38 | 39 | 40 | 41 |
Số giày | 3 | 9 | 2 | 1 |
Cỡ giày trung bình:
\(\bar X = \frac{{38.3 + 39.9 + 40.2 + 41}}{{3 + 9 + 2 + 1}} = \frac{{586}}{{15}} \approx 39\)
Ý nghĩa: Cỡ giày trung bình này có thể đại diện cho cỡ giày của cửa hàng.
b) Cỡ giày số 39 là cỡ giày nhiều khách nam đi nhất trong tổng số người được chọn nên cửa hàng nên nhập cỡ giày này.

Đáp án B.
Số quần bán được là 379 chiếc
⇒ Số trung vị M e là số chính giữa của dãy khi xếp số quần bán được thành một dãy không giảm
⇒ M e là quần có size đứng ở vị trí 190 ⇒ M e = 27

a) Năm 2019:
+) Số trung bình: \(\overline x = \frac{{54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31}}{{12}} = 33,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{54}^2} + {{22}^2} + ... + {{31}^2}} \right) - 33,{5^2} = 67,25\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 8,2\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 22, 24, 29, 29, 30, 31, 31, 35, 37, 40, 40, 54
\({Q_2} = {M_e} = \frac{1}{2}(31 + 31) = 31\)
\({Q_1}\) là trung vị của nửa số liệu: 22, 24, 29, 29, 30, 31. Do đó \({Q_1} = 29\)
\({Q_3}\) là trung vị của nửa số liệu: 31, 35, 37, 40, 40, 54. Do đó \({Q_3} = 38,5\)
\( \Rightarrow {\Delta _Q} = 38,5 - 29 = 9,5\)
Năm 2020:
+) Số trung bình: \(\overline x = 34,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{45}^2} + {{28}^2} + ... + {{37}^2}} \right) - 34,{5^2} = 15,75\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 3,97\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 28, 31, 32, 33, 33, 34, 34, 35, 35, 37, 37, 45.
\({Q_2} = {M_e} = \frac{1}{2}(34 + 34) = 34\)
\({Q_1}\) là trung vị của nửa số liệu: 28, 31, 32, 33, 33, 34. Do đó \({Q_1} = 32,5\)
\({Q_3}\) là trung vị của nửa số liệu: 34, 35, 35, 37, 37, 45. Do đó \({Q_3} = 36\)
\( \Rightarrow {\Delta _Q} = 36 - 32,5 = 3,5\)
b) Nhận xét:
So sánh số trung bình: số lượng bán ra trung bình theo tháng không tăng nhiều so với năm trước (tăng 1)
So sánh độ lệch chuẩn: Số lượng xe bán ra năm 2020 không có sự chênh lệch quá nhiều giữa các tháng.
=> Tác động của chiến lược: Số lượng xe bán ra tăng ít, nhưng đồng đều giữa các tháng.

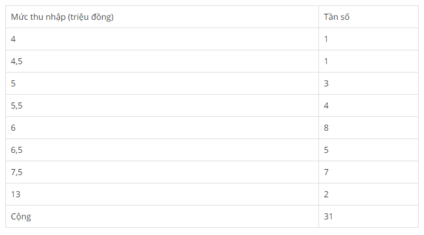
Số trung bình x = 6,6 triệu đồng. Số trung vị M e triệu đồng. Mốt M 0 = 6 triệu đồng.
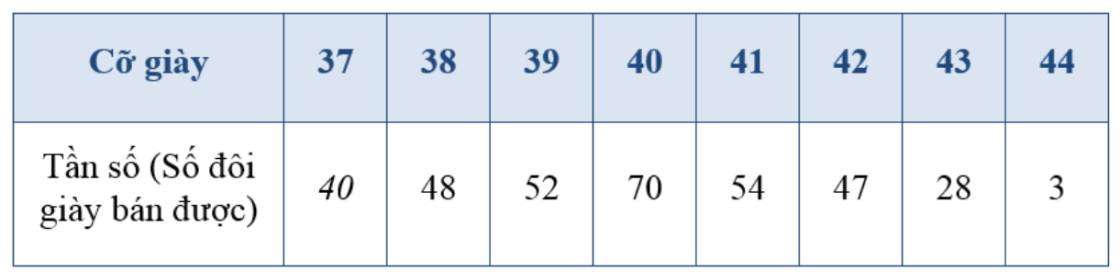

a) Ta thấy tần số lớn nhất là 70 và 70 ứng với cỡ giày 40 nên mốt của mẫu số liệu là: \({M_o} = 40\)
b) Do mốt là 40 nên cửa hàng đó nên nhập về nhiều hơn cỡ giày 40 để bán trong tháng tiếp theo.