K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1

NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
\(\Leftrightarrow2cos4x\left(cos2x-sin2x\right)=0\)
\(\Leftrightarrow cos4x=0\) (do \(cos4x=cos^22x-sin^22x\) đã bao hàm \(cos2x-sin2x\))
\(\Rightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
NH
0


CM
25 tháng 5 2018
Đáp án D
Nhận thấy rằng cosx=0=>sinx=1 không là nghiệm của phương trình đã cho nên ta có:
![]()
![]()

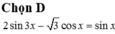
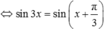
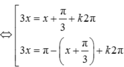
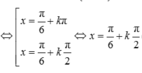



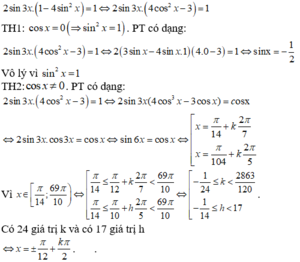
\(2sin3x+1=0\Leftrightarrow sin3x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-\dfrac{\pi}{6}+k2\pi\\3x=\dfrac{7\pi}{6}+n2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\\x=\dfrac{7\pi}{18}+\dfrac{n2\pi}{3}\end{matrix}\right.\)
\(x\in\left(-\dfrac{25\pi}{18};\dfrac{31\pi}{18}\right)\Rightarrow\left\{{}\begin{matrix}-\dfrac{25\pi}{18}< -\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\le< \dfrac{31\pi}{18}\\-\dfrac{25\pi}{18}< \dfrac{7\pi}{18}+\dfrac{n2\pi}{3}< \dfrac{31\pi}{18}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-2< k< \dfrac{8}{3}\\-\dfrac{8}{3}< n< 2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=\left\{-1;0;1;2\right\}\\n=\left\{-2;-1;0;1\right\}\end{matrix}\right.\)
\(\Rightarrow\) Pt có 8 nghiệm trên khoảng đã cho