Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Giá trị lớn nhất là: 653.
Giá trị bé nhất là: 492.
Khoảng biến thiên là: 653 - 492 = 161.
Để chia thành 7 nhóm có độ dài bằng nhau, ta lấy điểm đầu mút trái của nhóm đầu tiên là 492, điểm đầu mút phải của nhóm cuối là 653 với độ dài mỗi nhóm là 23.
Ta có mẫu số liệu ghép nhóm sau:


Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:


Tham khảo:
Do số quyển sách là số nguyên nên ta hiệu chỉnh lại như sau:

Số sách trung bình được mượn mỗi ngày sau khi ghép nhóm là:
\(\bar x = \frac{{3.18 + 6.23 + 15.28 + 27.33 + 22.38 + 14.43 + 5.48}}{{92}} \approx 34,6\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {30,5;35,5} \right)\).
Do đó: \({u_m} = 30,5;{n_{m - 1}} = 15;{n_m} = 27;{n_{m + 1}} = 22;{u_{m + 1}} - {u_m} = 35,5 - 30,5 = 5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 30,5 + \frac{{27 - 15}}{{\left( {27 - 15} \right) + \left( {27 - 22} \right)}}.5 \approx 34\)
Vậy số lượng sách được mượn mỗi ngày cao nhất là 35 quyển.

Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).

Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)

Vì đây là mẫu số liệu ghép nhóm và tần số các nhóm khác nhau nên có 1 mốt
Đáp án: B.

a, Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
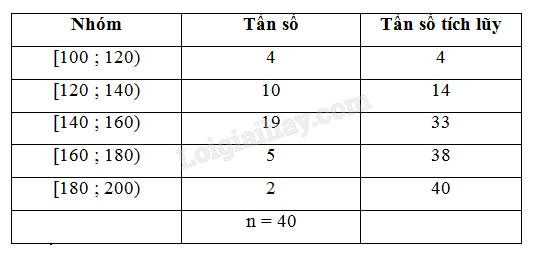
b, - Trung bình cộng là:
\(\overline{x}=\dfrac{110\cdot4+130\cdot15+150\cdot14+170\cdot5+190\cdot2}{40}=143\)
- Trung vị là: \(M_e=140+\left(\dfrac{20-19}{14}\right)\cdot20\simeq141\)
- \(Q_1=120+\left(\dfrac{10-4}{15}\right)\cdot20\simeq128\\ Q_2=M_e\simeq141\\ Q_3=140+\left(\dfrac{30-19}{15}\right)\cdot20=155,6\)
c, Mốt của mẫu số liệu là:
Có nhóm 2 là nhóm có tần số lớn nhất
\(\Rightarrow M_o=120+\left(\dfrac{15-4}{2\cdot15-4-14}\right)\cdot20\simeq138,3\)

Số cuộc gọi của người đó trong một tuần là \(n = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian thực hiện cuộc gọi của người đó trong một tuần được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \left[ {0;60} \right);{x_9},...,{x_{18}} \in \left[ {60;120} \right);{x_{19}},...,{x_{25}} \in \left[ {120;180} \right);{x_{26}},...,{x_{30}} \in \left[ {180;240} \right);\) \({x_{31}},{x_{32}} \in \left[ {240;300} \right);{x_{33}} \in \left[ {300;360} \right)\).
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{17}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {60;120} \right)}\end{array}\)
Ta có: \(n = 33;{n_m} = 10;C = 8;{u_m} = 60;{u_{m + 1}} = 120\)
Tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}.\left( {120 - 60} \right) = 111\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_8} + {x_9}} \right)\).
Do \({x_8} \in \left[ {0;60} \right),{x_9} \in \left[ {60;120} \right)\) nên tứ phân vị thứ nhất của dãy số liệu là: \({Q_1} = 60\).
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\).
Do \({x_{25}} \in \left[ {120;180} \right),{x_{26}} \in \left[ {180;240} \right)\) nên tứ phân vị thứ ba của dãy số liệu là: \({Q_3} = 180\).
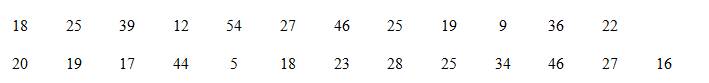
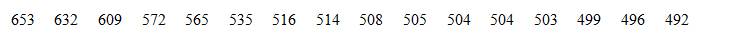








Tham khảo:
Giá trị nhỏ nhất là: 5.
Giá trị lớn nhất là 54.
Do đó khoảng biến thiên là 54 - 5 = 49.
Để chia thành 6 nhóm với độ dài bằng nhau ta lấy điểm đầu mút phải trái của nhóm đầu tiên là 3 và đầu mút phải của nhóm cuối cùng là 57 với độ dài mỗi nhóm là 9.
Ta được mẫu số liệu ghép nhóm như sau: