Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) A=1718+1/1719+1
17A=1719+17/1719+1
17A=1719+1+16/1719+1
17A=1+16/1719+1
Tương tự:
B=1717+1/1718+1
17B=1718+17/1718+1
17B=1718+1+16/1718+1
17B=1+16/1718+1
Vì 16/1719+1<16/1718+1 nên 17A<17B
⇒A<B
b) A=108-2/108+2
A=108+2-4/108+2
A=1+-4/108+2
Tương tự:
B=108/108+4
B=108+4-4/108+1
B=1+-4/108+1
Vì -4/108+2>-4/108+1 nên A>B
c)A=2010+1/2010-1
A=2010-1+2/2010-1
A=1+2/2010-1
Tương tự:
B=2010-1/2010-3
B=2010-3+2/2010-3
B=1+2/2010-3
Vì 2/2010-3>2/2010-1 nên B>A
⇒A<B
Chúc bạn học tốt!
17A=1719+1+16/1719+1
17A=1+16/1719+1
phần in nghiêng mình không hiểu lắm, bn giải thích cho mình được ko?

Ta có : \(A=\frac{10^{17}+5}{10^{17}-8}=\frac{10^{17}-8+13}{10^{17}-8}=1+\frac{13}{10^{17}-8}\)
Lại có B = \(\frac{10^{17}-13+13}{10^{17}-13}=1+\frac{13}{10^{17}-13}\)
Nhận thấy 1017 - 8 > 1017 - 13
=> \(\frac{13}{10^{17}-8}< \frac{13}{10^{17}-13}\)
=> \(1+\frac{13}{10^{17}-8}< 1+\frac{13}{10^{17}-13}\)
=> A < B

\(A=\frac{10^{17}+5}{10^{17}-8}=\frac{10^{17}-8+13}{10^{17}-8}=\frac{10^{17}-8}{10^{17}-8}+\frac{13}{10^{17}-8}=1+\frac{13}{10^{17}-8}\)
\(B=\frac{10^{17}}{10^{17}-3}=\frac{10^{17}-3+13}{10^{17}-3}=\frac{10^{17}-3}{10^{17}-3}+\frac{13}{10^{17}-3}=1+\frac{13}{10^{17}-3}\)
Nhận xét: \(10^{17}-8\frac{13}{10^{17}-3}\Rightarrow1+\frac{13}{10^{17}-8}>1+\frac{13}{10^{17}-3}\Rightarrow A>B\)
\(A=\frac{10^{17}+5}{10^{17}-8}=\frac{10^{17}-8+13}{10^{17}-8}=\frac{10^{17}-8}{10^{17}-8}+\frac{13}{10^{17}-8}=2+\frac{3}{10^{17}-8}\)
\(B=\frac{10^{17}}{10^{17}-3}=\frac{10^{17}-3+3}{10^{17}-3}=\frac{10^{17}-3}{10^{17}-3}+\frac{3}{10^{17}-3}=1+\frac{3}{10^{17}-3}\)
Do \(2+\frac{3}{10^{17}-8}>1+\frac{3}{10^{17}-3}\)n\(A>B\)

A=\(\frac{10^8+2}{10^8-1}=1+\frac{3}{10^8-1}\)
\(B=\frac{10^8}{10^8-3}=1+\frac{3}{10^8-3}\)
Vì\(10^8-1>10^8-3\)
\(\Rightarrow\frac{3}{10^8-1}< \frac{3}{10^8-3}\)
\(\Rightarrow1+\frac{3}{10^8-1}< 1+\frac{3}{10^8-3}\)
Vậy \(A< B\)

2:
a: =4+3/8+5+2/3
=9+3/8+2/3
=216/24+9/24+16/24
=216/24+25/24
=241/24
b; =2+3/8+1+1/4+3+6/7
=6+3/8+1/4+6/7
=6+5/8+6/7
=419/56
c: \(=2+\dfrac{3}{8}-1-\dfrac{1}{4}+5+\dfrac{1}{3}\)
=6+3/8-1/4+1/3
=6+1/8+1/3
=6+11/24
=155/24
d: \(=3+\dfrac{5}{6}+6\cdot\dfrac{13}{6}\)
=3+13+5/6
=16+5/6
=101/6
e: =3+1/2+4+5/7-5-5/14
=3+4-5+1/2+5/7-5/14
=2+7/14+10/14-5/14
=2+12/14
=2+6/7=20/7
f: =9/2+1/2:11/2
=9/2+1/11
=99/22+2/22=101/22

a, \(\dfrac{10}{17}\) + \(\dfrac{5}{-13}\) - \(\dfrac{11}{25}\) + \(\dfrac{7}{17}\) - \(\dfrac{8}{13}\)
= ( \(\dfrac{10}{17}\) + \(\dfrac{7}{17}\)) - ( \(\dfrac{5}{13}\) + \(\dfrac{8}{13}\)) - \(\dfrac{11}{25}\)
= \(\dfrac{17}{17}\) - \(\dfrac{13}{13}\) - \(\dfrac{11}{25}\)
= 1 - 1 - \(\dfrac{11}{25}\)
= - \(\dfrac{11}{25}\)
b, 0,3 - \(\dfrac{93}{7}\) - 70% - \(\dfrac{4}{7}\)
= 0,3 - 0,7 - ( \(\dfrac{93}{7}+\dfrac{4}{7}\))
= - 0,4 - \(\dfrac{97}{7}\)
= - \(\dfrac{2}{5}\) - \(\dfrac{97}{7}\)
= - \(\dfrac{499}{35}\)

`@` `\text {Ans}`
`\downarrow`
`a)`
\(\dfrac{1}{2}-\dfrac{5}{6}+\dfrac{11}{33}-\dfrac{35}{40}\)
`=`\(\dfrac{1}{2}-\dfrac{5}{6}+\dfrac{1}{3}-\dfrac{7}{8}\)
`=`\(\dfrac{12}{24}-\dfrac{20}{24}+\dfrac{8}{24}-\dfrac{21}{24}\)
`= -21/24 = -7/8`
`b)`
\(\dfrac{2}{3}\cdot1\dfrac{3}{4}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{2}{3}\cdot\dfrac{7}{4}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{7}{6}-\dfrac{8}{9}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(\dfrac{5}{18}-\dfrac{17}{51}-\dfrac{1}{5}\)
`=`\(-\dfrac{1}{18}-\dfrac{1}{5}=-\dfrac{23}{90}\)
`c)`
\(\dfrac{1}{2}\cdot2-2\dfrac{5}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(1-\dfrac{19}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(-\dfrac{12}{7}+\dfrac{6}{4}-\dfrac{10}{15}\)
`=`\(-\dfrac{3}{14}-\dfrac{10}{15}=-\dfrac{37}{42}\)
`d) `
\(\dfrac{1}{6}\cdot\dfrac{1}{11}+\dfrac{4}{11}\cdot\left(-\dfrac{1}{6}\right)+\dfrac{8}{11}\cdot\dfrac{1}{6}+\dfrac{1}{6}\cdot\dfrac{6}{11}\)
`=`\(\dfrac{1}{6}\cdot\left(\dfrac{1}{11}-\dfrac{4}{11}+\dfrac{8}{11}+\dfrac{6}{11}\right)\)
`=`\(\dfrac{1}{6}\cdot\left(\dfrac{1-4+8+6}{11}\right)\)
`=`\(\dfrac{1}{6}\cdot1=\dfrac{1}{6}\)
`e)`
\(-17\cdot\left(-23\right)+\left(-53\right)\cdot17+17\cdot14+17\cdot\left(-24\right)\)
`= 17*(23-53+14-24)`
`= 17*(-40)`
`= -680`
`f)`
\(-19\cdot218+\left(-82\right)\cdot19-533\cdot19+\left(-19\right)\cdot167\)
`= 19*(-218-82-533-167)`
`= 19*(-1000)`
`= -19000`
`g)`
\(\dfrac{2}{5}+\dfrac{3}{8}-\dfrac{11}{44}+\dfrac{9}{16}\)
`=`\(\dfrac{2}{5}+\dfrac{3}{8}-\dfrac{1}{4}+\dfrac{9}{16}\)
`=`\(\dfrac{31}{40}-\dfrac{1}{4}+\dfrac{9}{16}\)
`=`\(\dfrac{21}{40}+\dfrac{9}{16}=\dfrac{87}{80}\)
`h)`
\(\dfrac{4}{10}-1\dfrac{5}{6}\cdot2+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(\dfrac{4}{10}-\dfrac{11}{6}\cdot2+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(\dfrac{4}{10}-\dfrac{11}{3}+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(-\dfrac{49}{15}+\dfrac{7}{8}-\dfrac{1}{9}\)
`=`\(-\dfrac{287}{120}-\dfrac{1}{9}=-\dfrac{901}{360}\)
`i )`
\(3\cdot\dfrac{1}{5}-\dfrac{2}{8}-\dfrac{12}{36}+\dfrac{15}{9}\)
`=`\(\dfrac{3}{5}-\dfrac{1}{4}-\dfrac{1}{3}+\dfrac{15}{9}\)
`=`\(\dfrac{7}{20}-\dfrac{1}{3}+\dfrac{15}{9}\)
`=`\(\dfrac{1}{60}+\dfrac{15}{9}=-\dfrac{33}{20}\)
`k)`
\(\dfrac{6}{8}\cdot3\dfrac{1}{2}+4\dfrac{2}{3}-\dfrac{11}{55}+\dfrac{17}{51}\)
`=`\(\dfrac{3}{4}\cdot\dfrac{7}{2}+\dfrac{14}{3}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{21}{8}+\dfrac{14}{3}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{175}{24}-\dfrac{1}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{851}{120}+\dfrac{17}{51}=\dfrac{297}{40}\)
`l )`
\(\dfrac{1}{3}\cdot3\dfrac{1}{2}-4\dfrac{2}{5}-\dfrac{26}{78}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\cdot\dfrac{7}{2}-\dfrac{22}{5}-\dfrac{1}{3}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\left(\dfrac{7}{2}-1\right)-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{1}{3}\cdot\dfrac{5}{2}-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(\dfrac{5}{6}-\dfrac{22}{5}+\dfrac{17}{51}\)
`=`\(-\dfrac{107}{30}+\dfrac{17}{51}=-\dfrac{97}{30}\)
P/s: Bạn tách bài ra hỏi nhé! Và ghi đề rõ ràng chứ đừng ghi ntnay, nhiều bạn nhìn vào rất khó nhìn!
`# \text {KaizulvG}`
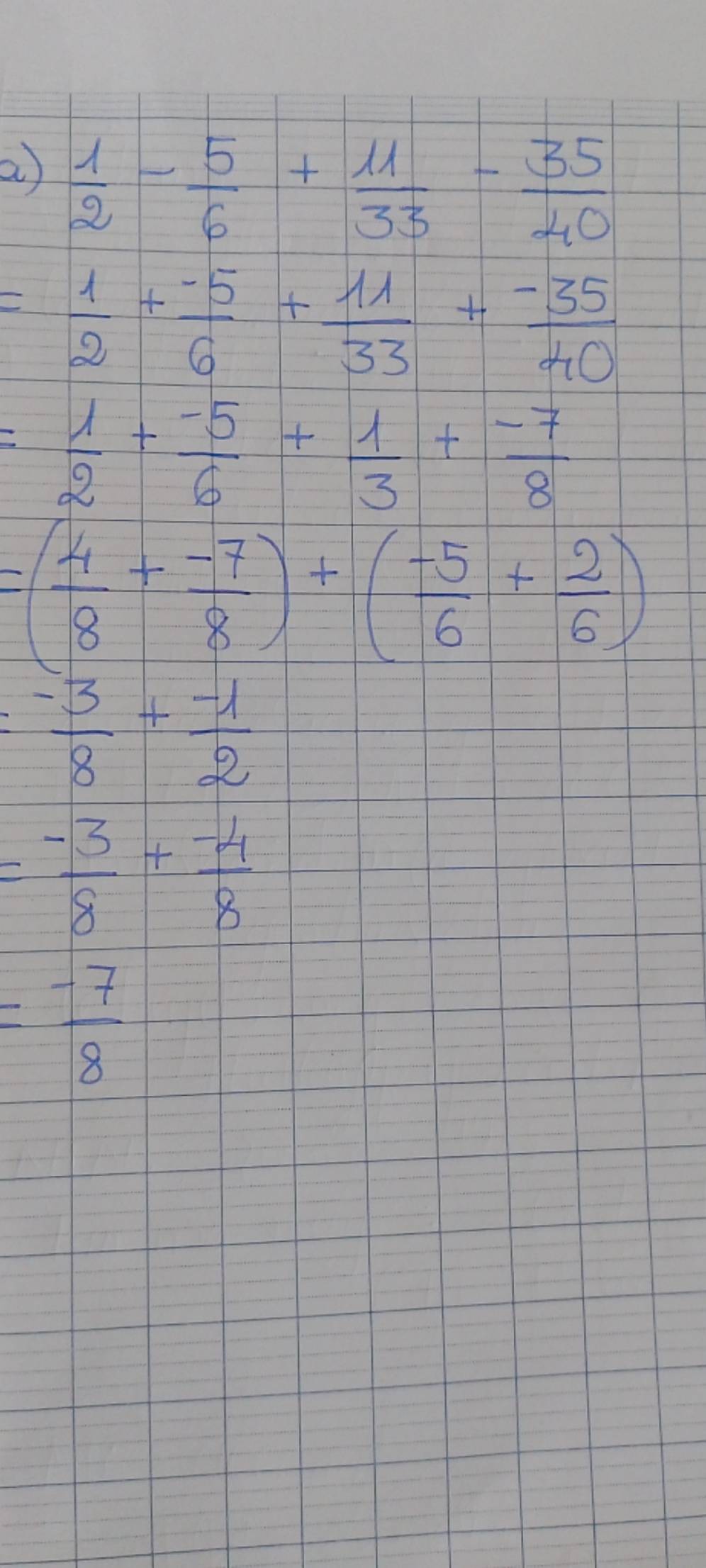
\(A=\frac{10^8+2}{10^8-1}=\frac{10^8-1+3}{10^8-1}=1+\frac{3}{10^8-1}\)
\(B=\frac{10^8}{10^8-3}=\frac{10^8-3+3}{10^8-3}=1+\frac{3}{10^8-3}\)
Nhận thầy 108 - 1 > 108 - 3
=> \(\frac{3}{10^8-1}< \frac{3}{10^8-3}\)
=> \(1+\frac{3}{10^8-1}< \frac{3}{10^8-3}+1\)
=> A < B
b) 17C = \(\frac{17\left(17^{203}+1\right)}{17^{204}+1}=\frac{17^{204}+1+16}{17^{204}+1}=1+\frac{16}{17^{204}+1}\)
17D = \(\frac{17\left(17^{202}+1\right)}{17^{203}+1}=\frac{17^{203}+1+16}{17^{203}+1}=1+\frac{16}{17^{203}+1}\)
Nhận thầy 17203 + 1 < 17204 + 1
=> \(\frac{16}{17^{203}+1}>\frac{16}{17^{204}+1}\)
=> \(\frac{16}{17^{203}+1}+1>\frac{16}{17^{204}+1}+1\Rightarrow17C>17D\Rightarrow C>D\)