
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 2^30= 2^3.10= (2^3)^10= 8^10
3^20= 3^2.10= (3^2)^10= 9^10
Vì 8<9 nên 8^10<9^10
=> 2^30<3^20

Ta có : A=2005^2005+1/2005^2006+1
=>2005A=2005.(2005^2005+1)/2005^2006+1
=>2005A=2005^2006+2005/2005^2006+1
=>2005A=2005^2006+1+2004/2005^2006+1
=>2005A=2005^2006+1/2005^2006+1 + 1/2005^2006+1
=>2005A=1+1/2005^2006+1
Lại có:B=2005^2004+1/2005^2005+1
=>2005B=2005.(2005^2004+1)/2005^2005+1
=>2005B=2005^2005+2005/2005^2005+1
=>2005B=2005^2005+1+2004/2005^2005+1
=>2005B=2005^2005+1/2005^2005+1 + 1/2005^2005+1
=>2005B=1+1/2005^2005+1
Vì 2006>2005
=>2005^2006>2005^2005
=>2005^2006+1>2005^2005+1
=>1/2005^2006+1<1/2005^2005+1
=>1+1/2005^2006+1<1+1/2005^2005+1
=>2005A<2005B
=>A<B
Vậy A<B
Ủng hộ mik nha mọi người !!!

ta có:
a=2-2^2+2^3-2^4+.....-2^98+2^99
bài trên có số số hạng
(99-2):1+1=98(số)
vậy dễ thấy:
2/2+2/99=2/101;2^3+2/98=2/101
vậy tổng tên là:
2-(2/101x98)=6/101
mà b chỉ có mẫu là 4
=> a lớn hơn b
Phải là 2 +.... chứ sao trừ :v
\(A=2+2^2+2^3+...+2^{99}\)
\(2A=2^2+2^3+...+2^{100}\)
\(2A-A=\left(2^2+2^3+...+2^{100}\right)-\left(2+2^2+...+2^{99}\right)\)
\(A=2^{100}-2=2\left(2^{99}-1\right)\)
\(B=1+4+4^2+...+4^{48}+4^{49}\)
\(B=1+4\left(1+4+4^2+...+4^{48}\right)\)
\(B=1+4\left(B-4^{49}\right)\)
\(B=1+4B-4^{50}\)
\(B=\frac{4^{50}-1}{3}\)
\(\frac{\left(2^2\right)^{50}-1}{3}=\frac{2^{100}-1}{3}>2^{100}-2\)

202³⁰³ = (202³)¹⁰¹ = 8242408¹⁰¹
303²⁰² = (303²)¹⁰¹ = 91809¹⁰¹
Do 8242408 > 91809 nên 8282408¹⁰¹ > 91809¹⁰¹
Vậy 202³⁰³ > 303²⁰²
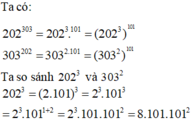
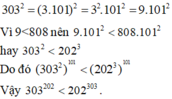
Ta có :
\(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
\(\Rightarrow202^{303}>303^{202}\)
202^303=(202^3)^101=8242408^101
303^202=(303^2)^101=91809^101
vì 8242408>91809 nên 8242408^101>91809^101
=>202^303>303^202