
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a. $2^{29}< 5^{29}< 5^{39}$
$\Rightarrow A< B$
b.
$B=(3^1+3^2)+(3^3+3^4)+(3^5+3^6)+...+(3^{2009}+3^{2010})$
$=3(1+3)+3^3(1+3)+3^5(1+3)+...+3^{2009}(1+3)$
$=(1+3)(3+3^3+3^5+...+3^{2009})$
$=4(3+3^3+3^5+...+3^{2009})\vdots 4$
Mặt khác:
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2008}+3^{2009}+3^{2010})$
$=3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2008}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+....+3^{2008})=13(3+3^4+...+3^{2008})\vdots 13$
Bài 1:
c.
$A=1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{99}-3^{100}+3^{101}$
$\Rightarrow A+3A=3^{101}+1$
$\Rightarrow 4A=3^{101}+1$
$\Rightarrow A=\frac{3^{101}+1}{4}$

\(\left(3^{2011}+3^{2010}\right):3^{2010}\)
\(=3^{2010}\left(3+1\right):3^{2010}\)
\(=4.3^{2010}:3^{2010}\)
\(=4\)
Ta có: \(\left(3^{2011}+3^{2010}\right):3^{2010}\)
=3+1
=4

Theo đề bài ra, ta có :
`A=1+32+34+36+....+32008`
\(\Rightarrow\) `9A = 3^2 + 3^4 + 3^6 + 3^8 + ... + 3^2010`
`9A - A=(32+34+36+38+....+ 32010)-(1+32+34+36+....+ 32008)`
\(\Rightarrow\) `8A=(-1)+32010`
\(\Rightarrow\) `8A-32010=(-1)`
@Nae

A = 32010 + 52010 cmr A ⋮ 13
A = 32010 + 52010 = (33)670 + (54)502.52 = 27670 + 625502.25
27 \(\equiv\) 1 (mod 13) ⇒ 27670 \(\equiv\) 1670 (mod 13) ⇒ 27670 \(\equiv\)1 (mod 13)
625 \(\equiv\) 1(mod 13) ⇒625502 \(\equiv\) 1502(mod 13) ⇒ 625502\(\equiv\) 1(mod 13)
25 \(\equiv\) -1 (mod 13)
625502 \(\equiv\) 1 (mod 13)
Nhân vế với vế ta được: 625502.25 \(\equiv\) -1 (mod 13)
Mặt khác ta có: 27670 \(\equiv\) 1 (mod 13)
Cộng vế với vế ta được:27670 + 625502.25 \(\equiv\) 1 -1 (mod 13 )
27670 + 625502.25 \(\equiv\) 0 (mod 13)
⇒ 27670 + 625502.25 ⋮ 13
⇒ A = 32010 + 52010 = 27670 + 625502.25 ⋮ 13 (đpcm)

viết rõ đề ra được ko bạn,mkko hiểu đề lắm
gọi x là tổng các chữ số của a= 3^2010+2011, gọi y là tổng các chữ số của x. gọi z là toonggr các chữ số của y. tìm z

a: 43/52>26/52=1/2=60/120
b: 17/68=1/4<1/3=35/105<35/103
c: \(\dfrac{2018\cdot2019-1}{2018\cdot2019}=1-\dfrac{1}{2018\cdot2019}\)
\(\dfrac{2019\cdot2020-1}{2019\cdot2020}=1-\dfrac{1}{2019\cdot2020}\)
2018*2019<2019*2020
=>-1/2018*2019<-1/2019*2020
=>\(\dfrac{2018\cdot2019-1}{2018\cdot2019}< \dfrac{2019\cdot2020-1}{2019\cdot2020}\)

\(\dfrac{19}{19}\) = 1 < \(\dfrac{2005}{2004}\) vậy \(\dfrac{19}{19}\) < \(\dfrac{2005}{2004}\)
\(\dfrac{72}{73}\) = 1 - \(\dfrac{1}{73}\)
\(\dfrac{98}{99}\) = 1 - \(\dfrac{1}{99}\)
Vì \(\dfrac{1}{73}\) > \(\dfrac{1}{99}\) nên \(\dfrac{72}{73}\) < \(\dfrac{98}{99}\)
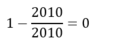
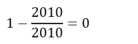
Ta có: \(3^{2010}=3^{10}\cdot3^{2000}=3^{10}\cdot9^{1000}\)
\(2^{3010}=2^{10}\cdot2^{3000}=2^{10}\cdot8^{1000}\)
Xét thấy \(3^{10}>2^{10};9^{1000}>8^{1000}\)
\(\Rightarrow3^{10}\cdot9^{1000}>2^{10}\cdot8^{1000}\)
Vậy \(3^{2010}>2^{3010}\)