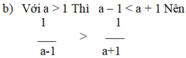
Ta thấy :

1/a-1 < 1/a

và 1/a < 1/a+1

nên theo theo tính chất bắc cầu ta có :

1/a-1 < 1/a < 1/a+1

=> 1/a-1 < 1/a+1

Vậy 1/a-1 < 1/a+1

\(\frac{1}{a}-1< \frac{1}{a}+1\)

hok tốt !

a. Vì  2008 2009 < a ; 10 9 > 1 nên  2008 2009 < 10 9

b. Với a > 1 Thì   a – 1 < a + 1 Nên

1 a - 1 > 1 a + 1

ta có:\(\frac{2005}{2004}-1=\frac{1}{2004}\)

        \(\frac{14}{13}-1=\frac{1}{13}\)

Vì \(\frac{1}{2004}<\frac{1}{13}\)nên phân số \(\frac{2005}{2004}<\frac{14}{13}\)

\(\frac{a}{x-1}>\frac{a}{x+1}\) vì x-1<x+1

2005 phần 2004 > 14 phần 13

a phần x - 1 > a phần x + 1

a) C1 : Ta có : \(\frac{11}{12}=1-\frac{1}{12}\)

\(\frac{12}{13}=1-\frac{1}{13}\)

Vì \(\frac{1}{12}>\frac{1}{13}\Rightarrow1-\frac{1}{12}< 1-\frac{1}{13}\Rightarrow\frac{11}{12}< \frac{12}{13}\)

C2 : \(\frac{11}{12}=\frac{143}{156}\)

\(\frac{12}{13}=\frac{144}{156}\)

Vì 143 < 144

=> \(\frac{143}{156}< \frac{144}{156}\Leftrightarrow\frac{11}{12}< \frac{12}{13}\)

b) C1: Ta có : \(\frac{71}{69}=1+\frac{2}{69}\)

\(\frac{69}{67}=1+\frac{2}{67}\)

Vì \(\frac{2}{69}< \frac{2}{67}\Rightarrow1+\frac{2}{69}< 1+\frac{2}{67}\Rightarrow\frac{71}{69}< \frac{69}{67}\)

C2) Ta có : \(\frac{69}{67}-\frac{71}{69}=\frac{4761}{4623}-\frac{4757}{4623}=\frac{4}{4623}>0\)

=> \(\frac{69}{67}-\frac{71}{69}>0\)

=> \(\frac{69}{67}>\frac{71}{69}\)

thanks

So sánh \(\frac{2005}{2004}và\frac{14}{13}\)

Ta có: \(\frac{2005}{2004}-1=\frac{1}{2004}\)

\(\frac{14}{13}-1=\frac{1}{13}\)

Vì \(\frac{1}{2004}< \frac{1}{13}\Rightarrow\frac{2005}{2004}< \frac{14}{13}\)

So sánh \(\frac{A}{X-1}và\frac{A}{X+1}\)

Vì X - 1 < X + 1 mà hai phân số có cùng tử số

\(\Rightarrow\frac{A}{X-1}>\frac{A}{X+1}\)

2005/2004<14/13 còn cái kia thì mình chịu

\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2019.2020}\)

\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-...+\frac{1}{2019}-\frac{1}{2020}\)

\(=1-\frac{1}{2020}>1\)

Thank you bạn dcv new ^ ^