
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận thấy \(y=0\) không phải nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}x^3-2x^2y+3y=0\\2xy^2-y^3-3y=0\end{matrix}\right.\)
\(\Rightarrow x^3-2x^2y+2xy^2-y^3=0\)
\(\Leftrightarrow\left(x-y\right)^3+xy\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2-xy+y^2\right)=0\)
\(\Leftrightarrow x=y\Rightarrow2x^2-x^2=3\Rightarrow x=y=\pm\sqrt{3}\)

Gọi 2 cạnh góc vuông là `AB,AC`, cạnh huyền là `BC`, đường cao `AH`.
Có: `(AB)/(AC)=3/7 = (3x)/(7x) (x>0)`
Áp dụng hệ thức lượng trong tam giác vuông ABC:
`1/(AH^2)=1/(AB^2)+1/(AC^2)`
`<=>1/(42^2)=1/(9x^2)+1/(49x^2)`
`=> x=2\sqrt58(cm)`
`=> AB=6\sqrt58, AC=14\sqty58 (cm)`
Áp dụng định lí Pytago:
`AB^2=HB^2+AH^2`
`<=> (6\sqrt58)^2=HB^2+42^2`
`=> HB=18(cm)`
`=> HC = AH^2 : HB = 98(cm)`
Vậy `HB=18cm, HC=98cm`.

ĐKXĐ: ...
Đặt \(\sqrt{2x-1}=t\ge0\Rightarrow x=\frac{t^2+1}{2}\)
\(\Rightarrow A=\frac{2t^2+6t+4}{t^2+4t+3}=\frac{2\left(t+1\right)\left(t+2\right)}{\left(t+1\right)\left(t+3\right)}=\frac{2\left(t+2\right)}{t+3}=2-\frac{2}{t+3}\ge2-\frac{2}{3}=\frac{4}{3}\)
Dấu "=" xảy ra khi \(t=0\Leftrightarrow x=\frac{1}{2}\)

quy đồng H lên rồi rút gọn
sau ko rút gọn xong thì tìm x nguyên khi H=6

\(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}=3\\ \Leftrightarrow\frac{x^2z}{xyz}+\frac{y^2x}{xyz}+\frac{z^2y}{xyz}=3\\ \Leftrightarrow x^2z+y^2x+z^2y=3xyz\\ \Leftrightarrow x^2z+y^2x+z^2y-3xyz=0\\ \Leftrightarrow xz\left(x-y\right)+yx\left(y-z\right)+yz\left(z-x\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}xz\left(x-y\right)=0\\yx\left(y-z\right)=0\\yz\left(z-x\right)=0\end{matrix}\right.\Leftrightarrow\left(x,y,z>0\Rightarrow xz,yx,yz\ne0\right)\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\Leftrightarrow x=y=z\Rightarrow1+1+1=3\left(dpcm\right)\)
Mình bổ sung tí TH2:\(\frac{\sqrt{y}}{x}+\frac{\sqrt{z}}{y}+\frac{\sqrt{x}}{z}=\frac{\sqrt{x}}{x}+\frac{\sqrt{x}}{x}+\frac{\sqrt{x}}{x}=\frac{3}{\sqrt{x}}\le3\)

Viết công thức toán ở dấu giống chữ E ngoài cùng bên trái khung soạn thảo đó bạn, click vào đó chọn ô thứ 4 từ bên phải qua là chỗ viết hệ.
\(x^2-xy-2y^2=0\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=0\\x-2y=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-y\\x=2y\end{matrix}\right.\)
Thay xuống pt dưới:
\(\Rightarrow\left[{}\begin{matrix}2\left(-y\right)^2-3y\left(-y\right)+y+2y+y^2=9\\8y^2-6y^2-2y+2y+y^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}6y^2+3y=0\\3y^2=0\end{matrix}\right.\) \(\Rightarrow...\)

bài 1:hệ đối xứng nên trừ theo vế2 pt
\(\Rightarrow\left(x-y\right)\left(x^2+xy+y^2-1\right)=0\)
*)Xét x=y (easy)
*)Xét \(x^2+xy+y^2-1=0\) thì \(x^2+y^2+xy=1\)
Từ \(pt\left(1\right)\Rightarrow y=2-x^3\) thay vào có:
\(x^6-x^4-4x^3+x^2+2x+3=0\)
\(\Leftrightarrow\left(x^3-x-1\right)^2+\left(x^2-x-\frac{3}{4}\right)^2+\frac{\left(2x-3\right)^2}{8}+\frac{5}{16}>0\)
vô nghiệm
động não nghĩ thôi,sắp ra rồi,ối lại quên rồi,a,sắp ra rồi!Huhu,lại quên rồi.........

\(\sqrt{xy}\le\dfrac{x+y}{2}\Rightarrow\dfrac{1}{\sqrt{xy}}\ge\dfrac{2}{x+y}\)
\(\Rightarrow A\ge\dfrac{1}{x}+\dfrac{2}{x+y}=2\left(\dfrac{1}{2x}+\dfrac{1}{x+y}\right)\ge2.\dfrac{4}{2x+x+y}=\dfrac{8}{3x+y}\ge\dfrac{8}{4}=2\)
\(A_{min}=2\) khi \(x=y=1\)
 somebody help me plz =))
somebody help me plz =))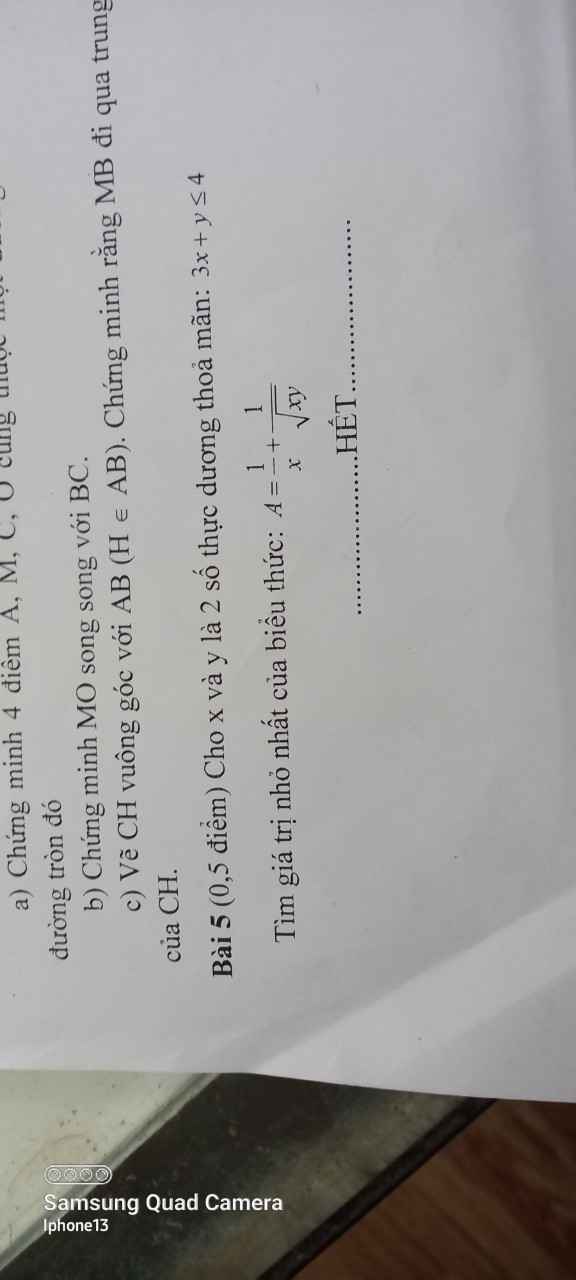
b, Gọi \(\left(d_3\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(P\left(1;3\right)\in\left(d_3\right)\Leftrightarrow a+b=3\left(1\right)\\ \left(d_3\right)\perp\left(d_1\right)\Leftrightarrow2a=-1\Leftrightarrow a=-\dfrac{1}{2}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)
Vậy đt cần tìm là \(y=-\dfrac{1}{2}x+\dfrac{7}{2}\)
c, Gọi \(\left(d\right):y=cx+d\left(c\ne0\right)\) là đt của (d)
\(\left(d\right)//Ox\Leftrightarrow d=y\\ C\left(0;2\right)\in\left(d\right)\Leftrightarrow d=2=y\\ \Leftrightarrow\left(d\right):y=2\)
PTHDGD của (d) và (d1) là \(2x=2\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\Leftrightarrow OA=1\)
PTHDGD của (d) và (d2) là \(\dfrac{1}{2}x=2\Leftrightarrow x=4\Leftrightarrow y=2\Leftrightarrow B\left(4;2\right)\Leftrightarrow OB=4\)
\(AB=OA+OB=5\)
Gọi D là chân đường cao từ O tới AB
\(\Leftrightarrow OD=2\) (do \(D\in\left(d\right):y=2\))
Vậy \(S_{ABO}=\dfrac{1}{2}OD\cdot AB=5\left(đvdt\right)\)